Understanding the receptive field of deep convolutional networks

On this article, we are going to talk about a number of views that contain the receptive discipline of a deep convolutional structure. We’ll handle the affect of the receptive discipline beginning for the human visible system. As you will notice, a whole lot of terminology of deep studying comes from neuroscience. As a brief motivation, convolutions are superior however it’s not sufficient simply to grasp the way it works. The thought of the receptive discipline will make it easier to dive into the structure that you’re utilizing or creating. In case you are searching for an in-depth evaluation to grasp how one can calculate the receptive discipline of your mannequin in addition to the simplest methods to extend it, this text was made for you. Ultimately, fundamentals are to be mastered! Let’s start.

Based on Wikipedia [1], the receptive discipline (of a organic neuron) is “the portion of the sensory area that may elicit neuronal responses, when stimulated”. The sensory area may be outlined in any dimension (e.g. a 2D perceived picture for an eye fixed). Merely, the neuronal response may be outlined because the firing charge (i.e. variety of motion potentials generated by a neuron). It’s associated to the time dimension based mostly on the stimuli. What’s vital is that it impacts the acquired frames per second (FPS) of our visible system. It isn’t clear what’s the actual FPS of our visible system, and it’s positively altering in numerous conditions (i.e. after we are at risk). Wikipedia [2] says:

Perception: The human visible system can course of 10 to 12 pictures per second and understand them individually, whereas increased charges are perceived as movement.

Let’s observe this picture to additional make clear these ideas:

The visible human system. Supply: brainconnection

Based mostly on the picture, all the space (the grid within the determine) an eye fixed can see is known as the sphere of view. The human visible system consists of tens of millions of neurons, the place every one captures totally different data. We outline the neuron’s receptive discipline as the patch of the whole discipline of view. In different phrases, what data a single neuron has entry to. That is in easy phrases the organic cell’s receptive discipline.

Let’s see how we will prolong this concept in convolutional networks.

For a holistic overview on laptop imaginative and prescient with deep studying, we advocate the “Deep Studying for Imaginative and prescient Techniques” e book. Use the low cost code aisummer35 to get an unique 35% low cost out of your favourite AI weblog.

What’s the receptive discipline in deep studying?

Equally, in a deep studying context, the Receptive Subject (RF) is outlined as the scale of the area within the enter that produces the function[3]. Mainly, it’s a measure of affiliation of an output function (of any layer) to the enter area (patch). Earlier than we transfer on, let’s make clear one vital factor:

Perception: The thought of receptive fields applies to native operations (i.e. convolution, pooling).

receptive-field-in-convolutional-networks

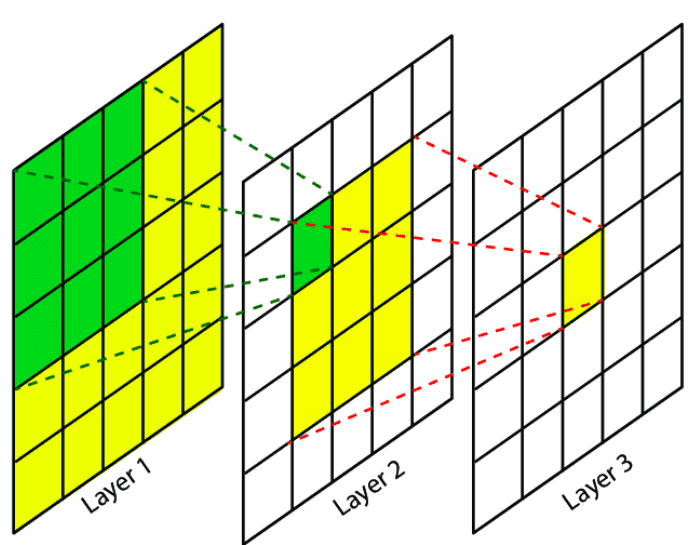
Supply: Analysis Gate

A convolutional unit solely depends upon a neighborhood area (patch) of the enter. That’s why we by no means check with the RF on absolutely linked layers since every unit has entry to all of the enter area. To this finish, our goal is to offer you an perception into this idea, with a view to perceive and analyze how deep convolutional networks work with native operations work.

Okay, however why ought to anybody care concerning the RF?

Why will we care concerning the receptive discipline of a convolutional community?

There is no such thing as a higher technique to make clear this than a few laptop imaginative and prescient examples. Specifically, let’s revisit a few dense prediction laptop imaginative and prescient duties. Particularly, in picture segmentation and optical circulation estimation, we produce a prediction for every pixel within the enter picture, which corresponds to a brand new picture, the semantic label map. Ideally, we wish every output pixel of the label map to have a giant receptive discipline, in order to make sure that no essential data was not taken under consideration. As an illustration, if we need to predict the boundaries of an object (i.e. a automobile, an organ like the center, a tumor) it will be important that we offer the mannequin entry to all of the related elements of the enter object that we need to section. Within the picture beneath, you possibly can see two receptive fields: the inexperienced and the orange one. Which one would you wish to have in your structure?

receptive-fields-semantic-segmentation

The inexperienced and orange rectangles are two totally different receptive fields. Which one would you favor? The inexperienced and orange rectangles are two totally different receptive fields. Which one would you favor? Supply: Nvidia’s weblog

Equally, in object detection, a small receptive discipline could not have the ability to acknowledge massive objects. That’s why you often see multi-scale approaches in object detection. Moreover, in motion-based duties, like video prediction and optical circulation estimation, we need to seize massive motions (displacements of pixels in a 2D grid), so we need to have an sufficient receptive discipline. Particularly, the receptive discipline needs to be enough whether it is bigger than the most important circulation magnitude of the dataset.

Subsequently, our aim is to design a convolutional mannequin in order that we be certain that its RF covers all the related enter picture area.

To persuade you much more, within the diagram beneath you possibly can see the relation of the RF to the classification accuracy in ImageNet. The radius refers back to the quantity of floating-point operations (FLOPs) of every mannequin. The purple corresponds to the ResNet [4] household (50-layer, 101, and 152 layers), whereas the yellow is the inception [5] household (v2, v3, v4). Gentle-blue is the MobileNet structure.

imagenet-classification-and-receptive-field

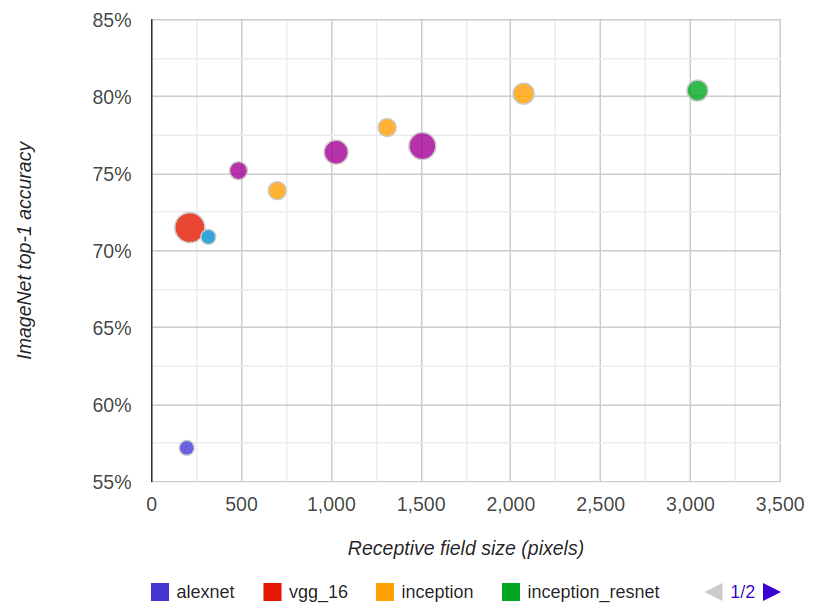
Picture is borrowed from Araujo et al. [3]

As completely described by Araujo et al. [3]:

“We observe a logarithmic relationship between classification accuracy and receptive discipline measurement, which suggests that enormous receptive fields are obligatory for high-level recognition duties, however with diminishing rewards.”

Nonetheless, the receptive discipline measurement alone shouldn’t be the one issue contributing to improved recognition efficiency. Nonetheless, the purpose is that you need to positively pay attention to your mannequin’s receptive discipline.

Okay, so how can we measure it?

Closed-form calculations of the receptive discipline for single-path networks

Within the wonderful work by Araujo et al. [3], they supply an intuitive technique to calculate in an analytical kind the RF of your mannequin. A single path actually means no skip connections within the structure, just like the well-known AlexNet. Let’s see some math! For 2 sequential convolutional layers $f2 , f1$

r_1 = s_2 instances r_2 + (k_2-s_2)

Or in a extra normal kind:

r_{(i-1)} = s_{i} instances r_{i} + (k_{i}-s_{i})

The picture beneath could make it easier to make clear this equation. Word that we have an interest to see the affect of the receptive discipline ranging from the final layer in direction of the enter. So, in that sense, we go backwards.

receptive-field-1d-conv-visualization

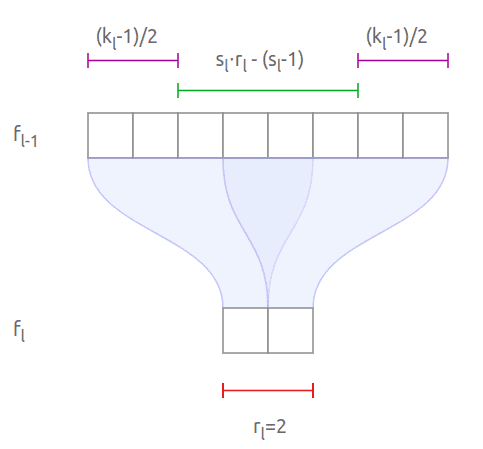
1D sequential conv. Layers visualization taken from Araujo et al. [3]

It looks like this equation may be generalized in an exquisite compact equation that merely applies this operation recursively for L layers. By additional analyzing the recursive equation, we will derive a closed kind resolution that relies upon solely on the convolutional parameters of kernels and strides [3]:

r_0 = sum_{i=1}^{L} ( (k_{i} -1) prod_{j=1}^{l-1} s_{j} ) + 1 quad quad (eq.1)

The place $r_0$

Okay, I measured the theoretical RF of my mannequin. Now, how can I improve it?

How can we improve the receptive discipline in a convolutional community?

In essence, there are a plethora of the way and tips to extend the RF, that may be summarized as follows:

Add extra convolutional layers (make the community deeper)
Add pooling layers or increased stride convolutions (sub-sampling)
Use dilated convolutions
Depth-wise convolutions

Let’s have a look at the distinct traits of those approaches.

Add extra convolutional layers

Possibility 1 will increase the receptive discipline measurement linearly, as every additional layer will increase the receptive discipline measurement by the kernel measurement [7]. Furthermore, it’s experimentally validated that because the theoretical receptive discipline is growing however the efficient (experimental) receptive discipline is decreasing. RF refers back to the RF, whereas ERF corresponds to the efficient RF.

Effective-receptive-field-ratio-with-more-layers

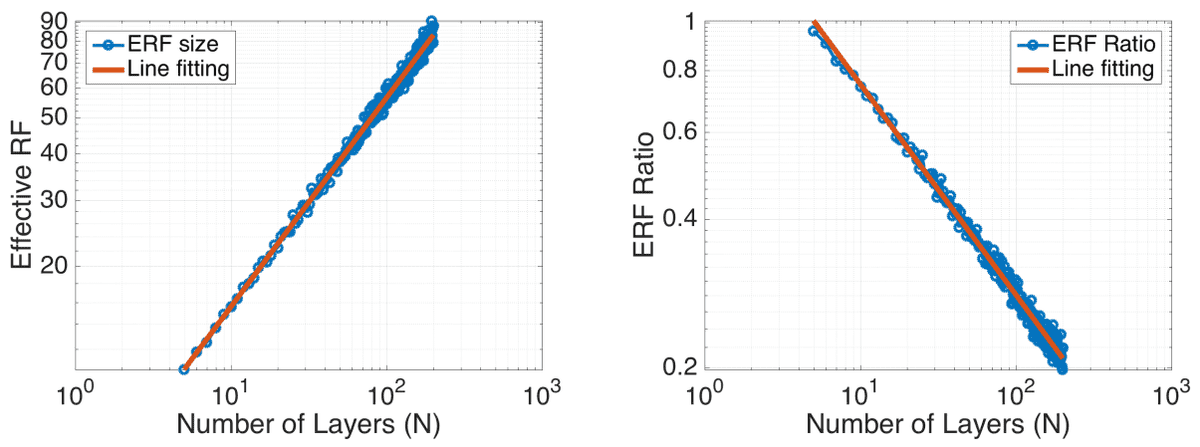
Growing the variety of layers decreases the ERF ration, taken from Luo et al. [7]

Sub-sampling and dilated convolutions

Sub-sampling strategies like pooling (choice 2) alternatively, will increase the receptive discipline measurement multiplicatively. Trendy architectures like ResNet mix these strategies(choice 1 and a pair of). However, sequentially positioned dilated convolutions, improve the RF exponentially.

However first, let’s revisit the concept of dilated convolutions.

In essence, dilated convolutions introduce one other parameter, denoted as r, referred to as the dilation charge. Dilations introduce “holes” in a convolutional kernel [3]. The “holes” mainly outline a spacing between the values of the kernel. So, whereas the variety of weights within the kernel is unchanged, the weights are now not utilized to spatially adjoining samples. Dilating a kernel by an element of $r$ introduces a sort of striding of $r$ .

The pre-described equations may be reused by merely changing the kernel measurement $ok$ for all layers utilizing dilations:

ok’= r (ok−1)+1

Hold this equation at the back of your thoughts.

All of the above may be illustrated within the following gif, produced by Dumoulin et al. 2016 [11]. I believe the picture speaks for itself:

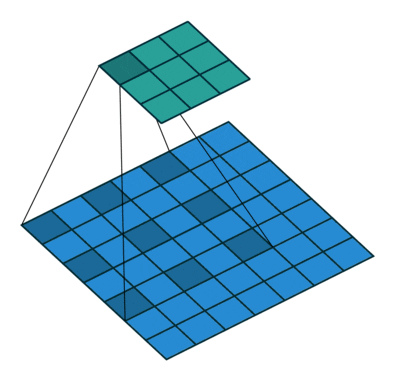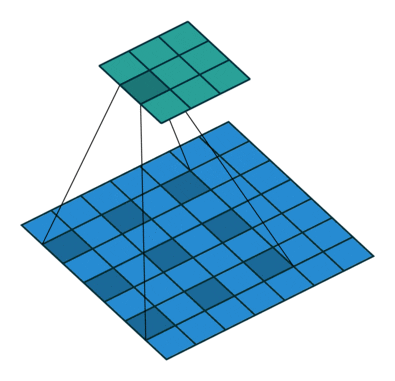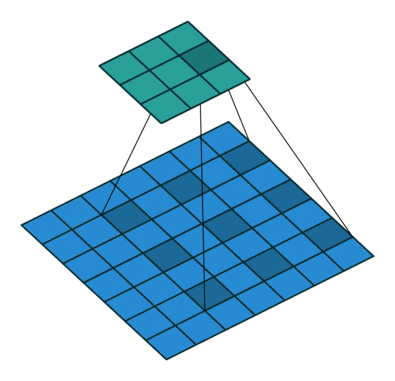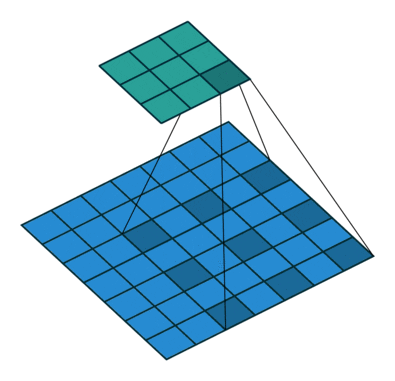convolutional-arithmetic Supply: A information to convolutional arithmetic Dumoulin et al. 2016 [11]

Now, let’s briefly examine how dilated convolutions can affect the receptive discipline.

Let’s see 3 sequential conv. Layers (denoted by a,b,c) which can be illustrated within the picture with regular convolution, r=2 dilation issue, and r=4 dilation issue. We’ll intuitively perceive why dilation helps an exponential growth of the receptive discipline with out lack of decision (i.e. pooling) or protection.

receptive-field-illustration-with-dilated-convs

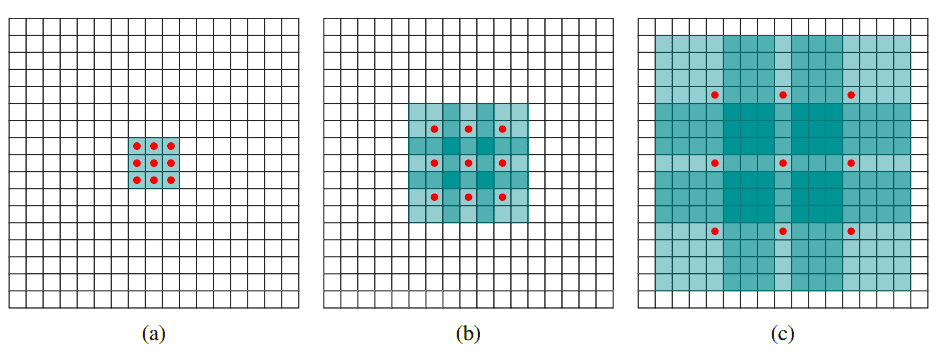
Picture is borrowed from Yu et al. 2015 [9]

Evaluation

In (a) we now have a standard 3×3 convolution with receptive discipline 3×3. In (b) we now have a 2-dilated 3×3 convolution that’s utilized within the output of layer (a) which is a standard convolution. In consequence, every aspect within the 2 coupled layers now has a receptive discipline of seven×7. If we studied 2-dilated conv alone the receptive discipline can be merely 5×5 with the identical variety of parameters. In (c) by making use of a 4-dilated convolution, every aspect within the third sequential conv layer now has a receptive discipline of 15×15. In consequence, the receptive discipline grows exponentially whereas the variety of parameters grows linearly [9].

In different phrases, a 3×3 kernel with a dilation charge of two can have the identical receptive discipline as a 5×5 kernel, whereas solely utilizing 9 parameters. Equally, a 3×3 kernel with a dilation charge of 4 can have the identical receptive discipline as a 9×9 kernel with out dilation. Mathematically:

r (ok −1)+1 = k_{prev}

Perception: In deep architectures, we regularly introduce dilated convolutions within the final convolutional layers.

Under you possibly can observe the ensuing ERF (efficient receptive discipline) when introducing pooling operation and dilation in an experimental examine carried out by [7]. Clearly, the receptive discipline is larger in each instances whereas with pooling it’s noticed to be bigger in a sensible setup. We’ll see extra concerning the efficient receptive discipline in a while.

Receptive-field-pooling-vs-dilated-conv

A visualization of the efficient receptive discipline (ERF) by introducing pooling methods and dilation, taken from Luo et al. 2016 [7]

Perception: Based mostly on [7], pooling operations and dilated convolutions transform efficient methods to extend the receptive discipline measurement shortly.

Lastly as described in Araujo et al. [3], with depth-wise convolutions the receptive discipline is elevated with a small compute footprint, so it’s thought of a compact technique to improve the receptive discipline with fewer parameters. Depthwise convolution is the channel-wise spatial convolution. Nonetheless, be aware that depth-wise convolutions don’t immediately improve the receptive discipline. However since we use fewer parameters with extra compact computations, we will add extra layers. Thus, with roughly the identical variety of parameters, we will get a much bigger receptive discipline. MobileNet [10] achieves excessive recognition efficiency based mostly on this concept.

Skip-connections and receptive discipline

If you wish to revisit the concepts behind skip connections, be at liberty to test my related article.

In a mannequin with none skip-connections, the receptive discipline is taken into account mounted. Nonetheless, when introducing $n$ skip-residual blocks, the networks make the most of $2^n$

histogram-high-res-net-receptive-field-distribution

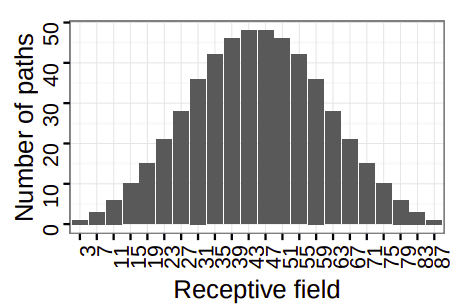
The histogram of receptive discipline distribution of HighResNet [8]

Perception: Skip-connections could present extra paths, nonetheless, based mostly on [7], they have an inclination to make the efficient receptive discipline smaller.

Receptive discipline and transposed convolutions, upsampling, separable convolutions, and batch normalization

Upsampling

Upsampling can also be a neighborhood operation. Concerning the RF computation functions may be thought of to have a kernel measurement equal to the variety of enter options concerned within the computation of an output function. Since we often double the spatial dimension, as proven within the determine beneath, the kernel is ok=1.

nearest-neighbour-upsampling

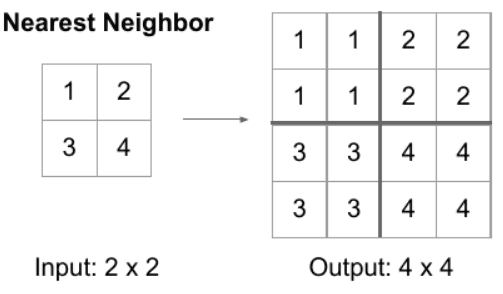
Upsampling borrowed from right here

Separable convolutions

In brief, the RF properties of the separable convolution are an identical to its corresponding equal non-separable convolution. So, virtually nothing modifications by way of the receptive discipline.

Batch normalization

Throughout coaching, batch normalization parameters are computed based mostly on all the channel parts of the function map. Thus, one can state that its receptive discipline is the entire enter picture.

Understanding the efficient receptive discipline

In [7], Luo et al. 2016 uncover that not all pixels in a receptive discipline contribute equally to an output unit’s response. Within the earlier picture, we noticed that the receptive discipline varies with skip connections.

Clearly, the output function shouldn’t be equally impacted by all pixels inside its receptive discipline. Intuitively, it’s straightforward to understand that pixels on the middle of a receptive discipline have a a lot bigger impression on output since they’ve extra “paths” to contribute to the output.

As a pure consequence, one can outline the relative significance of every enter pixel because the efficient receptive discipline (ERF) of the function. In different phrases, ERF defines the efficient receptive discipline of a central output unit as the area that incorporates any enter pixel with a non-negligible impression on that unit.

Particularly, as it’s referenced in [7] we will intuitively notice the contribution of central pixels within the ahead and backward go as:

“Within the ahead go, central pixels can propagate data to the output by way of many various paths, whereas the pixels within the outer space of the receptive discipline have only a few paths to propagate its impression. Within the backward go, gradients from an output unit are propagated throughout all of the paths, and due to this fact the central pixels have a a lot bigger magnitude for the gradient from that output.” ~ by Luo et al. 2016 [7].

A pure technique to measure this impression is after all the partial by-product, charge of change of the unit with respect to the enter, as it’s computed by backpropagation.

Effective-receptive-field-gaussian-distribution

The efficient receptive discipline with and with out non-linearities, borrowed from Luo et al. 2016 [7]

As it’s illustrated within the determine, the ERF is an ideal instance of a textbook 2D Gaussian distribution. Nonetheless, after we add non-linearities, we power the distribution to deviate from an ideal Gaussian. In easy phrases, when the pixel-value is zeroed with the ReLU, no path from the receptive discipline can attain the output, therefore the gradient is zero.

Based mostly on this examine the principle perception is the next:

Perception: The ERF in deep convolutional networks really grows quite a bit slower than we calculate in principle [7].

Final however not least, it’s tremendous vital to spotlight that after the coaching course of the ERF is elevated, minimizing the hole between the theoretical RF and the ERF earlier than coaching.

Conclusion

On this article, we inspected a number of points of the idea of the Receptive Subject. We easily began from the human visible methods in order to make the ideas crystally clear. We mentioned the closed-form math, skip connections in RF, and how one can improve it effectively. Based mostly on that, you possibly can implement the referenced design selections in your mannequin, whereas being conscious of its implications.

Lastly, the take-away key factors of this text are summarized beneath:

The thought of receptive fields applies to native operations.
We need to design a mannequin in order that it’s receptive discipline covers all the related enter picture area.
Through the use of sequential dilated convolutions the receptive discipline grows exponentially, whereas the variety of parameters grows linearly.
Pooling operations and dilated convolutions transform efficient methods to extend the receptive discipline measurement shortly.
Skip-connections could present extra paths, however are likely to make the efficient receptive discipline smaller.
The efficient receptive discipline is elevated after coaching.

As a closing be aware, the understanding of RF in convolutional neural networks is an open analysis matter that can present a whole lot of insights on why deep convolutional networks work so rattling awesomely.

Extra materials

As an extra useful resource on the interpretation and visualization of RF, I’d advise you to try Kobayashi et al. 2020 [12]. For our extra sensible reader, if you’d like a toolkit to robotically measure the receptive discipline of your mannequin in Pytorch in Tensorflow, we acquired your again. Lastly, for these of you who’re hungry for information and curious for bio-inspired ideas like me, particularly concerning the human visible system, you possibly can watch this extremely really useful beginning video:

Cited as:

@article{adaloglou2020receptive,
  title   = "Understanding the receptive discipline of deep convolutional networks",
  writer  = "Adaloglou, Nikolas",
  journal = "https://theaisummer.com/",
  yr    = "2020",
  url     = "https://theaisummer.com/receptive-field/"
}

References

[1] Wikipedia: Receptive discipline

[2] Wikipedia: Body charge: Human Imaginative and prescient

[3] Araujo, A., Norris, W., & Sim, J. (2019). Computing receptive fields of convolutional neural networks. Distill, 4(11), e21.

[4] He, Ok., Zhang, X., Ren, S., & Solar, J. (2016). Deep residual studying for picture recognition. In Proceedings of the IEEE convention on laptop imaginative and prescient and sample recognition (pp. 770-778).

[5] Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., & Wojna, Z. (2016). Rethinking the inception structure for laptop imaginative and prescient. In Proceedings of the IEEE convention on laptop imaginative and prescient and sample recognition (pp. 2818-2826).

[7] Luo, W., Li, Y., Urtasun, R., & Zemel, R. (2016). Understanding the efficient receptive discipline in deep convolutional neural networks. In Advances in neural data processing methods (pp. 4898-4906).

[8] Li, W., Wang, G., Fidon, L., Ourselin, S., Cardoso, M. J., & Vercauteren, T. (2017, June). On the compactness, effectivity, and illustration of 3D convolutional networks: mind parcellation as a pretext process. In Worldwide convention on data processing in medical imaging (pp. 348-360). Springer, Cham.

[9] Yu, F., & Koltun, V. (2015). Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122.

[10] Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., … & Adam, H. (2017). Mobilenets: Environment friendly convolutional neural networks for cellular imaginative and prescient functions. arXiv preprint arXiv:1704.04861.

[11] Dumoulin, Vincent, and Francesco Visin. “A information to convolution arithmetic for deep studying.” arXiv preprint arXiv:1603.07285 (2016).

[12] Kobayashi, G., & Shouno, H. (2020). Interpretation of ResNet by Visualization of Most well-liked Stimulus in Receptive Fields. arXiv preprint arXiv:2006.01645.

* Disclosure: Please be aware that a number of the hyperlinks above is perhaps affiliate hyperlinks, and at no extra price to you, we are going to earn a fee in the event you determine to make a purchase order after clicking by way of.