Understanding SWAV: self-supervised learning with contrasting cluster assignments

Self-supervised studying goals to extract illustration from unsupervised visible knowledge and it’s tremendous well-known in laptop imaginative and prescient these days. This text covers the SWAV methodology, a strong self-supervised studying paper from a mathematical perspective. To that finish, we offer insights and intuitions for why this methodology works. Moreover, we’ll talk about the optimum transport downside with entropy constraint and its quick approximation that may be a key level of the SWAV methodology that’s hidden once you learn the paper.

In any case, if you wish to be taught extra about normal points of self-supervised studying, like augmentation, intuitions, softmax with temperature, and contrastive studying, seek the advice of our earlier article.

SWAV Methodology overview

Definitions

Let two picture options $mathbf{z}_t$

Supply: BYOL

• Our precise targets: Let $mathbf{q}_t$

• Prototypes: take into account a set of $Okay$ prototypes ${mathbf{c}_1, .., mathbf{c}_K}$

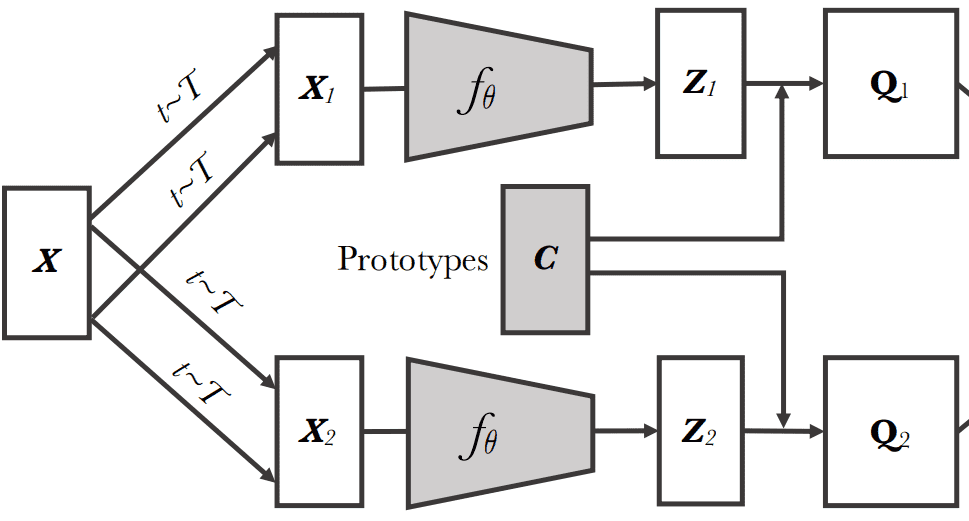
Supply: SWAV paper, Caron et al 2020

Clusters and prototypes are used interchangeably all through this text. Don’t confuse it with “codes” although! Nonetheless, codes and assignments are additionally used interchangeably.

SWAV ^{compares the options $mathbf{z}_t$}

Instinct: If $mathbf{z}_t$

Supply: SWAV’s github web page

Distinction between SWAV and SimCLR

In contrastive studying strategies, the options from completely different transformations of the identical photos are in contrast instantly to one another. SWAV does not instantly evaluate picture options. Why?

In SwAV, there may be the intermediate “codes” step ($Q$). To create the codes (targets), we have to assign the picture options to prototype vectors. We then clear up a “swapped” prediction downside whereby the codes (targets) are altered for the 2 picture views.

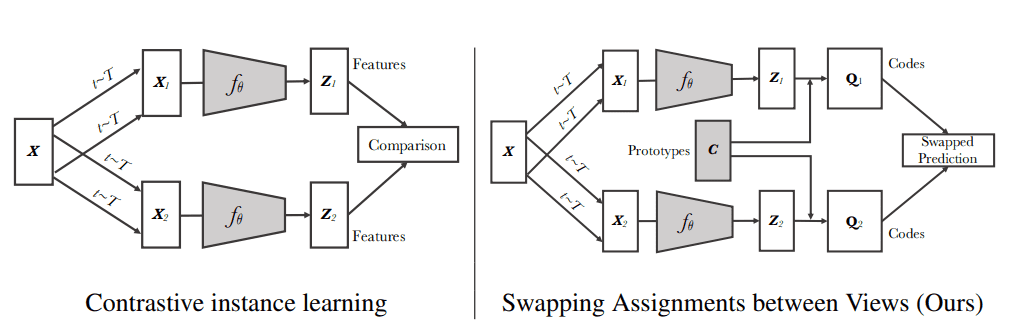
Supply: SWAV paper, Caron et al 2020

Prototype vectors ${mathbf{c}_1, .., mathbf{c}_K}$

The unit sphere and its implications

By definition, a unit sphere is the set of factors with L2 distance equal to 1 from a set central level, right here the origin. Notice that that is completely different from a unit ball, the place the L2 distance is lower than or equal to 1 from the centre.

Shifting on the floor of the sphere corresponds to a clean change in assignments. In actual fact many self-supervised strategies are utilizing this L2-norm trick, and particularly contrastive strategies. SWAV additionally applies L2-normalization to the options in addition to to the prototypes all through coaching.

SWAV methodology Steps

Let’s recap the steps of SWAV:

1. Create $N$ views from enter picture $X$ utilizing a set of stochastic transformations $T$

2. Calculate picture characteristic representations $z$

3. Calculate softmax-normalized similarities between all $z$ and $c$: $softmax(z^T c)$

4. Calculate code matrix $Q$ iteratively. We deliberately ignored this half. See additional on for this step.

5. Calculate cross-entropy loss between illustration $t$, aka $z_t$

6. Common loss between all $N$ views.

Supply: SWAV paper, Caron et al 2020

Once more, discover the distinction between cluster assignments (codes) and cluster prototype vectors ($c$). Here’s a detailed rationalization of the loss operate:

Digging into SWAV’s math: approximating Q

Understanding the Optimum Transport Downside with Entropic Constraint

As mentioned, the code vectors $mathbf{q}_1,…,mathbf{q}_B$

For $Okay$ prototypes and batch measurement $B$, the optimum code matrix $mathbf{Q} = [mathbf{q}_1,…,mathbf{q}_B] in R^{Okay instances B}$

For a proper and really detailed formulation, evaluation and answer of stated downside, I like to recommend taking a look on the paper ^.

For SwAV, we outline the optimum code matrix $mathbf{Q}$ as:

with $H$ being the entropy $H(mathbf{Q}) = – sum_{ij} mathbf{Q}_{ij} log mathbf{Q}_{ij}$

The hint $textual content{Tr}$ is outlined to be the sum of the weather on the principle diagonal.

A matrix $mathbf{Q}$ from the set $mathcal{Q}$ is constrained in 3 ways:

1. All its entries must be optimistic.

2. The sum of every row must be $1/Okay$

3. The sum of every column must be $1/B$.

4. Notice that this additionally implies that the sum of all entries to be $1$, therefore these matrices enable for a probabilistic interpretation, for instance, w.r.t. Entropy. Nevertheless, it’s not a stochastic matrix.

A easy matrix on this set is a matrix whose entries are all $1/(BK)$, which corresponds to a uniform distribution over all entries. This matrix maximizes the entropy $H(Q)$.

With a great instinct on the set $mathcal{Q}$, we are able to study the goal operate.

Optimum transport with out entropy

Ignoring the entropy-term for now, we are able to go step-by-step by means of the primary time period

Since each $mathbf{C}$ and $mathbf{Z}$ are L2 normalized, the matrix product $mathbf{C}^T mathbf{Z}$ computes the cosine similarity scores between all potential combos of characteristic vectors $mathbf{z}_1,…,mathbf{z}_B$

The primary column of $mathbf{C}^T mathbf{Z}$ accommodates the similarity scores for the primary characteristic vector $mathbf{z}_1$

Because of this the primary diagonal entry of $mathbf{Q}^T mathbf{C}^T mathbf{Z}$

Whereas its entropy time period can be:

Equally, the second diagonal entry of $mathbf{Q}^T mathbf{C}^T mathbf{Z}$

Doing this for all diagonal entries and taking the sum leads to $textbf{Tr}(mathbf{Q}^T mathbf{C}^T mathbf{Z})$

Instinct: Whereas the optimum matrix $mathbf{Q}^*$ is extremely non-trivial, it’s simple to see that $mathbf{Q}^*$ will assign giant weights to bigger similarity scores and small weights to smaller ones whereas conforming to the row-sum and column-sum constraint.

Primarily based on this design, such a way would be extra biased to mode collapse by selecting one prototype than collapsing to a uniform distribution.

Resolution? Implementing entropy to the rescue!

The entropy constraint

So why do we want the entropy time period in any respect?

Effectively, whereas the ensuing code vectors $mathbf{q}_1,…,mathbf{q}_B$

For $varepsilon rightarrow infty$

When $varepsilon = 0$

Lastly, small values for $varepsilon$ end in a barely smoothed $mathbf{Q}^*$.

Revisiting the constraints for $mathcal{Q}$, the row-sum and column-sum constraints suggest an equal quantity of whole weight is assigned to every prototype and every characteristic vector respectively.

The constraints impose a robust regularization that leads to avoiding mode collapse, the place all characteristic vectors are assigned to the identical prototype on a regular basis.

On-line estimation of Q* for SWAV

What’s left now’s to compute $mathbf{Q}^*$ in each iteration of the coaching course of, which fortunately seems to be very environment friendly utilizing the outcomes of ^.

Utilizing Lemma 2 from web page 5, we all know that the answer takes the shape:

the place $mathbf{u}$ and $mathbf{v}$ act as column and row normalization vectors respectively. An actual computation right here is inefficient. Nevertheless, the $textbf{Sinkhorn-Knopp}$ algorithm offers a quick, iterative different. We will initialize a matrix $mathbf{Q}$ because the exponential time period from $mathbf{Q}^*$ after which alternate between normalizing the rows and columns of this matrix.

Sinkhorn-Knopp Code evaluation

Right here is the pseudocode, given by the authors on the approximation of Q from the similarity scores:

def sinkhorn(scores, eps=0.05, niters=3):
Q = exp(scores / eps).T
Q /= sum(Q)
Okay, B = Q.form
u, r, c = zeros(Okay), ones(Okay) / Okay, ones(B) / B
for _ in vary(niters):
    u = sum(Q, dim=1) 
    Q *= (r / u).unsqueeze(1) 
    Q *= (c / sum(Q, dim=0)).unsqueeze(0) 
return (Q / sum(Q, dim=0, keepdim=True)).T

To approximate $Q$, we take as enter solely the similarity rating matrix $C^T Z$ and output our estimation for $Q$.

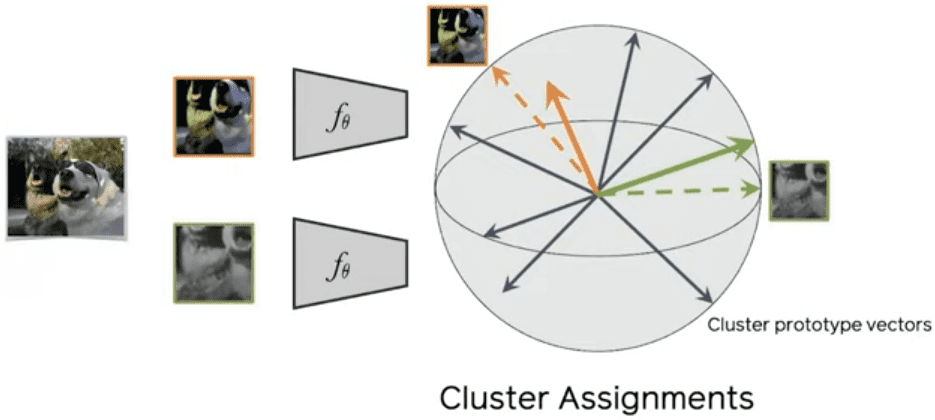
Instinct on the clusters/prototypes

So what is definitely discovered in these clusters/prototypes?

Effectively, the prototypes’ most important function is to summarize the dataset. So SWAV is nonetheless a type of contrastive studying. In actual fact, it will also be interpreted as a approach of contrasting picture views by evaluating their cluster assignments as a substitute of their options.

In the end, we distinction with the clusters and not the entire dataset. SimCLR makes use of batch info, referred to as unfavorable samples, however it’s not at all times consultant of the entire dataset. That makes the SWAV goal extra tractable.

This may be noticed from the experiments. In comparison with SimCLR, SWAV pretraining converges quicker and is much less delicate to the batch measurement. Furthermore, SWAV just isn’t that delicate to the variety of clusters. Sometimes 3K clusters are used for ImageNet. Generally, it is suggested to make use of roughly one order of magnitude bigger than the actual class labels. For STL10 which has 10 courses, 512 clusters can be sufficient.

The multi-crop concept: augmenting views with smaller photos

Each time I examine contrastive self-supervised studying strategies I believe, why simply 2 views? Effectively, the apparent query is answered within the SWAV paper additionally.

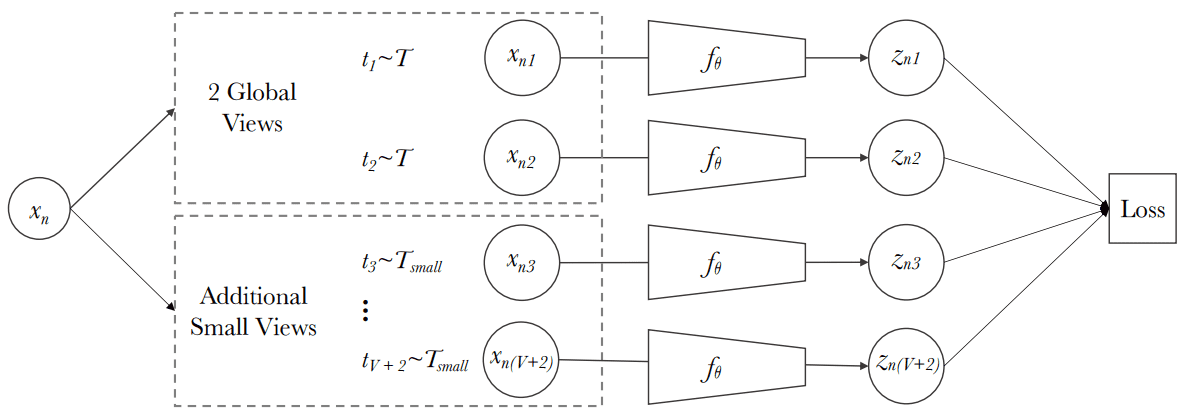
Multi-crop. Supply: SWAV paper, Caron et al 2020

To this finish, SwAV proposes a multi-crop augmentation technique the place the identical picture is cropped randomly with 2 international (i.e. 224×224) views and $N=4$

As proven beneath, multi-crop is a really normal trick to enhance self-supervised studying representations. It may be used out of the field for any methodology with surprisingly good outcomes ~2% enchancment on SimCLR!

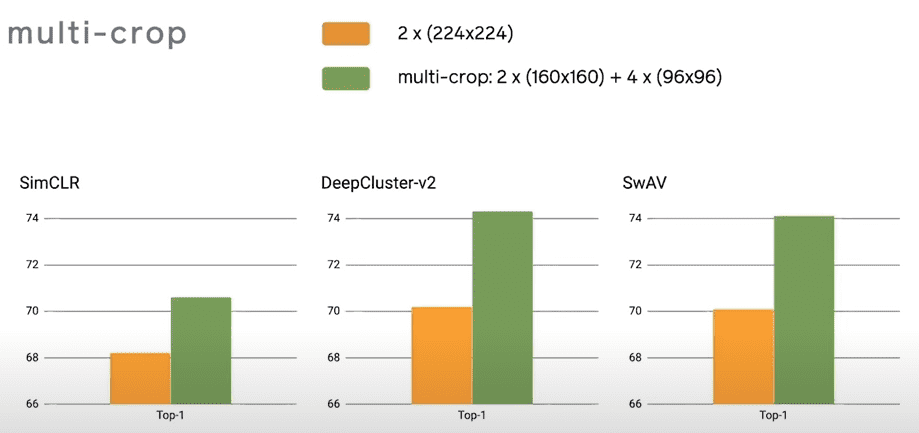
Supply: SWAV paper, Caron et al 2020

The authors additionally noticed that mapping small elements of a scene to extra international views considerably boosts the efficiency.

Outcomes

To judge the discovered illustration of $f$, the spine mannequin i.e. Resnet50 is frozen. A single linear layer is educated on high. This can be a honest comparability for the discovered representations, referred to as linear analysis. Under are the outcomes of SWAV in comparison with different state-if-the-art-methods.

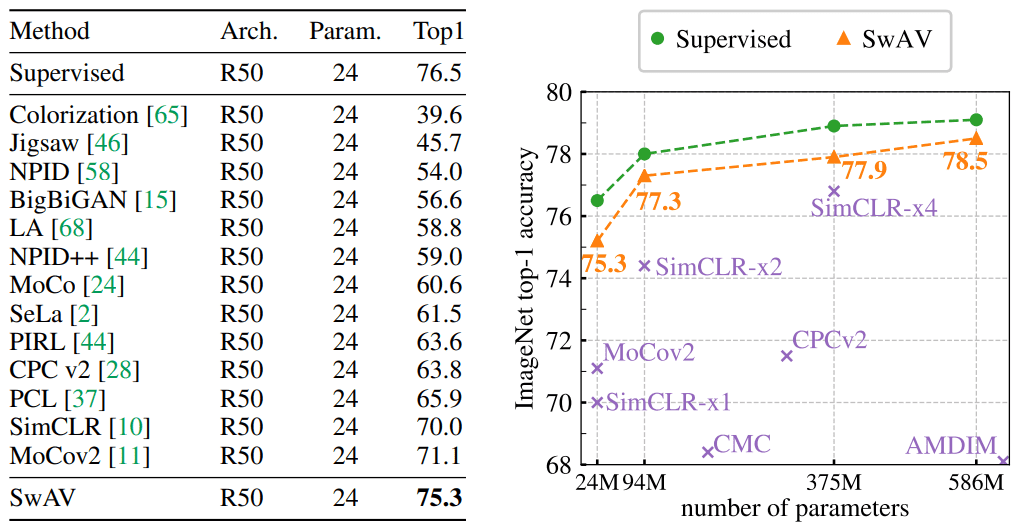
(left) Comparability between clustering-based and contrastive occasion strategies and
impression of multi-crop. (proper) Efficiency as a operate of epochs. Supply: SWAV paper, Caron et al 2020

Left: Classification accuracy on ImageNet is reported. The linear layers are educated on frozen options from completely different self-supervised strategies with a normal ResNet-50. Proper: Efficiency of extensive ResNets-50 by components of two, 4, and 5.

Conclusion

On this publish an summary of SWAV and its hidden math is offered. We lined the main points of optimum transport with and with out the entropy constraint. This publish wouldn’t be potential with out the detailed mathematical evaluation of Tim.

Lastly you may try this interview on SWAV by its first writer (Mathilde Caron).

For additional studying, check out self-supervised illustration studying on movies or SWAV’s experimental report. You may even run your individual experiments with the official code when you have a multi-GPU machine!

Lastly, I’ve to say that I’m a bit biased on the work of FAIR on visible self-supervised studying. This staff actually rocks!

References

1. SWAV Paper

2. SWAV Code

3. Ref paper on optimum transport

4. SWAV’s Report in WANDB

5. Optimum Transport downside

Cite as:

@article{kaiser2021swav,
    title   = "Understanding SWAV: self-supervised studying with contrasting cluster assignments",
    writer  = "Kaiser, Tim and Adaloglou, Nikolaos",
    journal = "https://theaisummer.com/",
    12 months    = "2021",
    howpublished = {https://theaisummer.com/swav/},
  }

* Disclosure: Please observe that a few of the hyperlinks above could be affiliate hyperlinks, and at no extra value to you, we’ll earn a fee for those who determine to make a purchase order after clicking by means of.