Why multi-head self attention works: math, intuitions and 10+1 hidden insights

This text is for curious individuals who need to actually perceive why and the way self-attention works. Earlier than implementing, or solely explaining a brand new fancy paper with transformers I believed it could be fascinating to current numerous views on the eye mechanism.

After learning this subject for a few months I discovered many hidden intuitions that can provide that means to the content-based consideration mechanism.

Why am I taking the time to additional analyze self-attention?

Firstly as a result of I could not discover easy solutions to my apparent query why multi-head self-attention works. Secondly, as a result of many high researchers like hadamaru from Google mind contemplate it as an important formulation after 2018:

TL;DR

Curiously, there are two kinds of parallel computations hidden inside self-attention:

We are going to analyze each. Extra importantly, I’ll attempt to present completely different views as to why multi-head self-attention works!

Please go to my introductory articles on consideration and transformers for a high-level overview or our open-source lib for implementations.

Wish to construct your PyTorch fundamentals? Study from the perfect ones on find out how to construct Deep Studying fashions with PyTorch. Use the code aisummer35 to get an unique 35% low cost out of your favourite AI weblog!

Self-attention as two matrix multiplications

The mathematics

We are going to contemplate self dot-product consideration with out a number of heads to boost readability. Given our inputs

and trainable weight matrices:

• $d_{mannequin}$
• $d_k$
• $batch$ is the batch measurement
• $tokens$ is the variety of components that our sequence has.

We create 3 distinct representations ( the question, the important thing, and the worth):

Then, we are able to outline the eye layer as:

You is perhaps questioning the place is the eye weights. First, let’s make clear that the eye is carried out because the dot-product and is going on proper right here:

The upper the dot-product the upper the eye “weights” might be. That is why it’s thought-about a similarity measure. Let’s see inside the maths now.

An Intuitive illustration

For the primary illustration, we are going to contemplate a case whereby queries do not come from the identical sequences as keys and vectors. Let’s say the question is a sequence of 4 tokens and the sequence that we wish to affiliate with, accommodates 5 tokens.

Each sequences comprise vectors of the identical embedding dimension, which is $d_model =3$

Take a while to research the next picture:

Picture by Writer

By placing all of the queries collectively, we have now a matrix multiplication as an alternative of a single question vector to matrix multiplication each time. Every question is processed utterly independently from the others. That is the parallelization that we get without cost by simply utilizing matrix multiplications and feeding all of the enter tokens/queries.

The Question-Key matrix multiplication

Content material-based consideration has distinct representations. The question matrix within the consideration layer is conceptually the “search” within the database. The keys will account for the place we might be trying whereas the values will really give us the specified content material. Think about the keys and values as parts of our database.

Intuitively, the keys are the bridge between the queries (what we’re on the lookout for) and the values (what we are going to really get).

Remember the fact that every vector to vector multiplication is a dot-product similarity. We will use the keys to information our “search” and inform us the place to look with respect to the enter components.

In different phrases, the keys will account for the computation of the eye on find out how to weigh the values based mostly on our explicit queries.

Discover that I didn’t present the softmax operation within the diagram, neither the scale-down issue $sqrt{d_{okay}}$

The eye V matrix multiplication

Then the weights $alpha_{ij}$

Cross consideration of the vanilla transformer

The identical rules apply within the encoder-decoder consideration or alternatively cross consideration, which makes full sense:

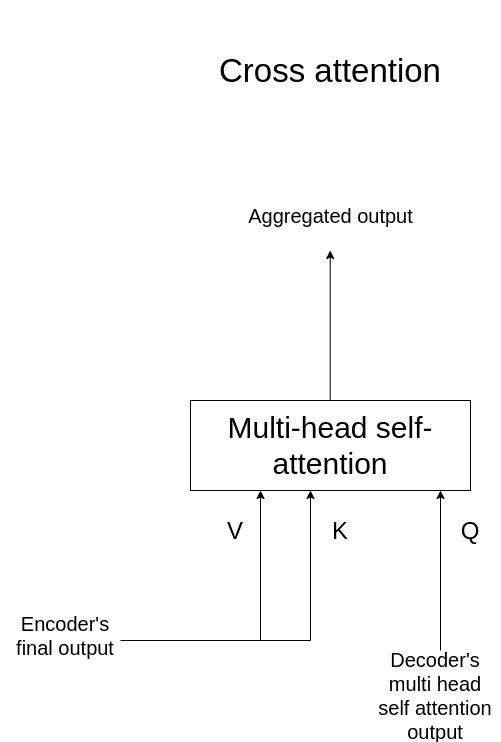
Illustration of cross consideration. Picture by Writer.

The keys and values are calculated by a linear projection of the ultimate encoded enter illustration, after a number of encoder blocks.

How multi-head consideration works intimately

Decomposing the eye in a number of heads is the second a part of parallel and impartial computations. Personally, I like to consider it as a number of “linear views” of the identical sequence.

The unique multi-head consideration was outlined as:

Principally, the preliminary embedding dimension $dim$ is decomposed to $h instances d_{head}$

See my article on implementing the self-attention mechanism for hands-on understanding on this topic.

The impartial consideration ‘heads’ are often concatenated and multiplied by a linear layer to match the specified output dimension. The output dimension is usually the identical because the enter embedding dimension $dim$. This permits a better stacking of a number of transformer blocks in addition to id skip connections.

I discovered an superior illustration of the a number of heads from Peltarion’s blogpost:

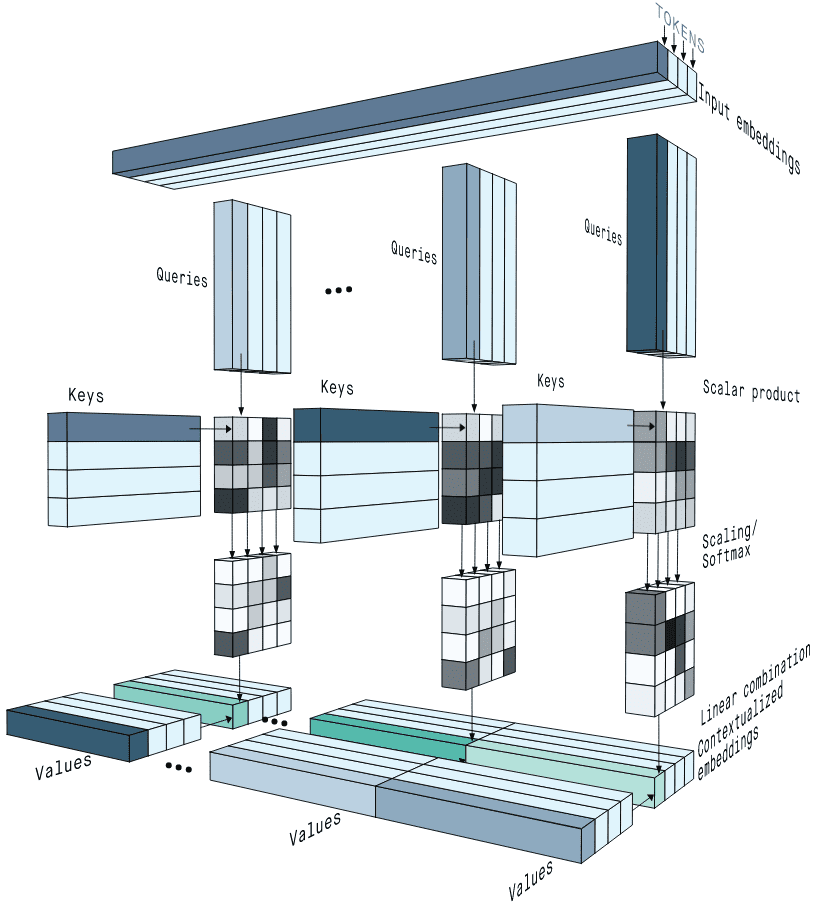
Supply: Getting that means from textual content: self-attention step-by-step video, Peltarion blogpost

Intuitively, a number of heads allow us to attend independently to (elements of) the sequence.

For those who like math and input-output diagrams, we obtained your again:

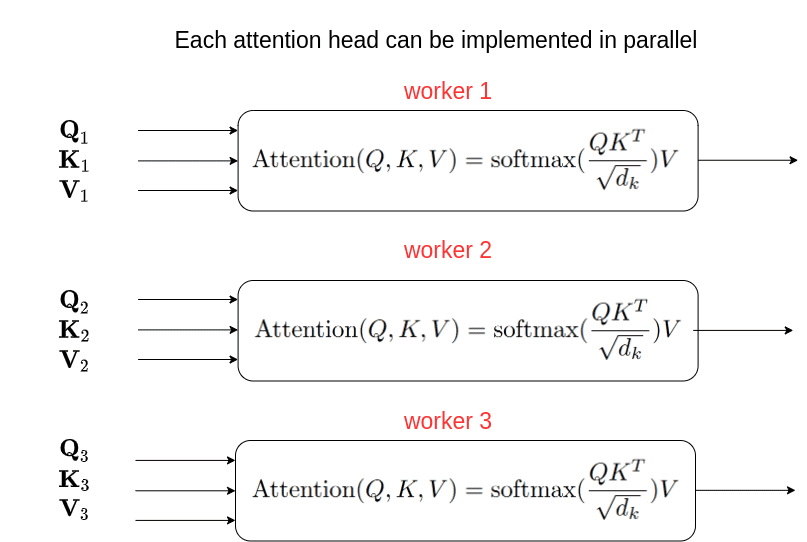
Picture by Writer

On the parallelization of impartial computations of self-attention

Once more, all of the representations are created from the identical enter and merged collectively to provide a single output. Nevertheless, the person $Q_{i}, K_{i}, V_{i}$

Usually, impartial computations have a very simple parallelization course of. Though, this will depend on the underlying low-level implementation within the GPU threads. Ideally, we might assign a GPU thread for every batch and for every head. As an example, if we had batch=2 and heads=3 we are able to run the computations in 6 completely different threads. Because the dimension is $d_k = d_{mannequin}/heads$

You most likely have been conscious of the speculation to date. Let’s delve into some fascinating observations.

Insights and observations on the eye mechanism

Self-attention will not be symmetric!

As a result of we have a tendency to make use of the identical enter illustration, don’t fall into the lure that self-attention is symmetric! I made this calamitous mistake once I began to know transformers.

Perception 0: self-attention is not symmetric!

For those who do the maths it turns into trivial to know:

Extra particularly, if the Keys and Queries have the identical quantity of $N$ tokens, the eye matrix $N instances N$

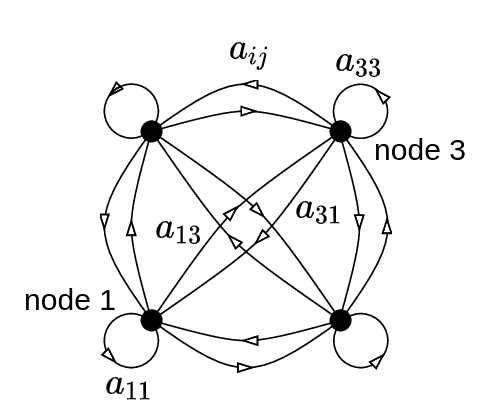
A totally-connected graph with 4 vertices and sixteen directed bonds.Picture from Gregory Berkolaiko. Supply: ResearchGate

The arrows that correspond to weights will be thought to be a type of data routing.

To ensure that the self-attention to be symmetric, we must use the identical projection matrix for the queries and the keys: $textbf{W}_Q = textbf{W}_K$

Why? As a result of while you multiply a matrix with its transpose you get a symmetric matrix. Nevertheless, remember the fact that the rank of the resulted matrix is not going to be elevated.

Impressed by this, there are lots of papers that use one shared projection matrix for the keys and the queries as an alternative of two. Extra on that on multi-head consideration.

Consideration because the routing of a number of native data

Based mostly on the ‘Enhancing the Transformer With Specific Relational Encoding for Math Drawback Fixing’ paper:

Perception 1: “This (their outcomes) signifies that the eye mechanism incorporates not only a subspace of the states it attends to, however affine transformations of these states that protect practically the total data content material. In such a case, the eye mechanism will be interpreted because the routing of a number of native data sources into one international tree construction of native representations.” ~ Schlag et al.

We are inclined to suppose that a number of heads will permit the heads to take care of completely different elements of the enter however this paper proves the preliminary guess improper. The heads protect nearly all of the content material. This renders consideration as a routing algorithm of the question sequence with respect to the important thing/values.

Encoder weights will be categorised and pruned effectively

In one other work, Voita et al. [4] analyzed what occurs when utilizing a number of heads of their work “Analyzing Multi-Head Self-Consideration: Specialised Heads Do the Heavy Lifting, the Relaxation Can Be Pruned”. They recognized 3 kinds of essential heads by taking a look at their consideration matrices:

1. Positional heads that attend largely to their neighbor.

2. Syntactic heads that time to tokens with a selected syntactic relation.

3. Heads that time to uncommon phrases within the sentence.

The easiest way to show the importance of their head categorization is by pruning the others. Right here is an instance of their pruning technique based mostly on the pinnacle classification for the 48 heads (8 heads instances 6 blocks) of the unique transformer:

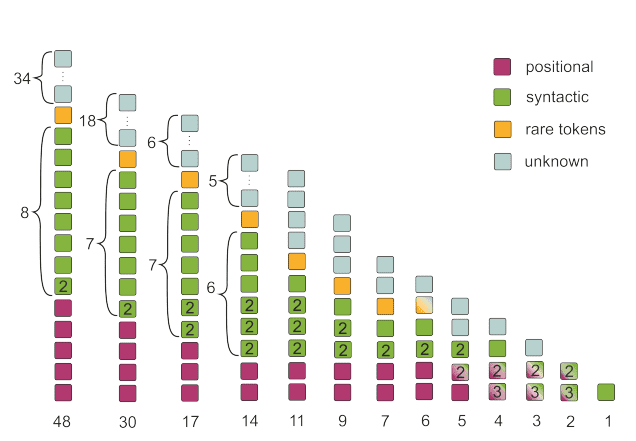
Picture by Voita et al. Supply: Analyzing Multi-Head Self-Consideration: Specialised Heads Do the Heavy Lifting, the Relaxation Can Be Pruned

By largely protecting the heads which can be categorised within the distinguished classes, as proven, they managed to retain 17 out of 48 heads with nearly the identical BLEU rating. Observe that this corresponds to roughly 2⁄3 of the heads of the encoder.

Under are the outcomes of pruning the Transformer’s encoder heads in two completely different datasets for machine translation:

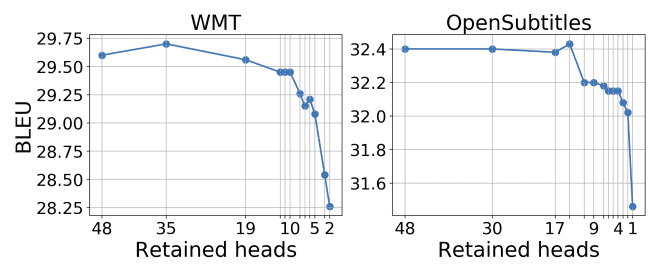
Picture by Voita et al. Supply: Analyzing Multi-Head Self-Consideration: Specialised Heads Do the Heavy Lifting, the Relaxation Can Be Pruned

Curiously, the encoder consideration heads have been the simplest to prune, whereas encoder-decoder consideration heads look like an important for machine translation.

Perception 2: Based mostly on the truth that the encoder-decoder consideration heads are retained largely within the final layers, it’s highlighted that the primary layers of the decoder account for language modeling, whereas the final layers for conditioning on the supply sentence.

Heads share widespread projections

One other precious paper on this course is “Multi-Head Consideration: Collaborate As a substitute of Concatenate” by Cordonnier et al.

The cumulative diagram depicts the sum of variances (in descending order for the X-axis) of the pretrained key and question matrices. The pretrained projection matrices are from a well-known NLP mannequin referred to as BERT with $dim_{head}=64$

The statement is predicated once more on this equation:

We might be trying into the pretrained projection product $textbf{W}_K^{T} textbf{X}^T$

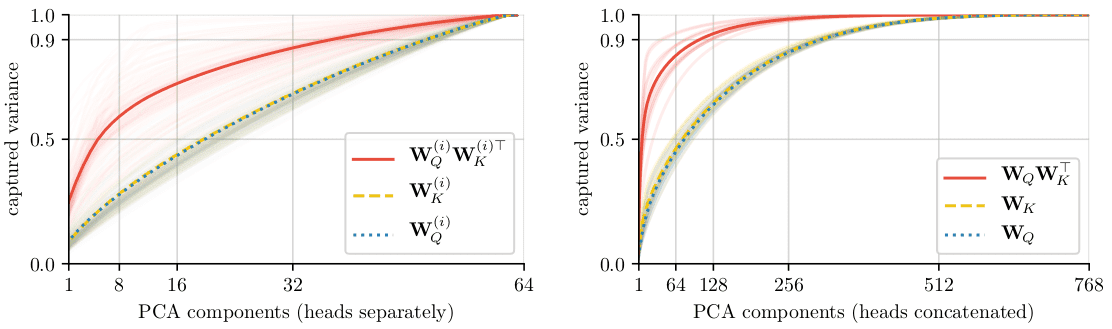
Picture by Cordonnier et al. Supply: Multi-Head Consideration: Collaborate As a substitute of Concatenate

The left determine depicts the product rank (in crimson) per head individually, whereas the suitable is per layer with concatenated heads.

Perception 3: Though the separate product of the load matrices per head is not low rank, the product of their concatenation (proven on the suitable, in crimson) is low rank.

This virtually implies that the heads share widespread projections. In different phrases, the phenomenally impartial heads in reality be taught to give attention to the identical subspaces.

A number of heads on the encoder-decoder consideration are tremendous essential

Paul Michel et al. [2] confirmed the significance of a number of heads when incrementally pruning heads from completely different consideration submodels.

The next determine reveals that efficiency drops rather more quickly when heads are pruned from the Encoder-Decoder consideration layers (cross consideration). The BLEU rating is reported for machine translation.

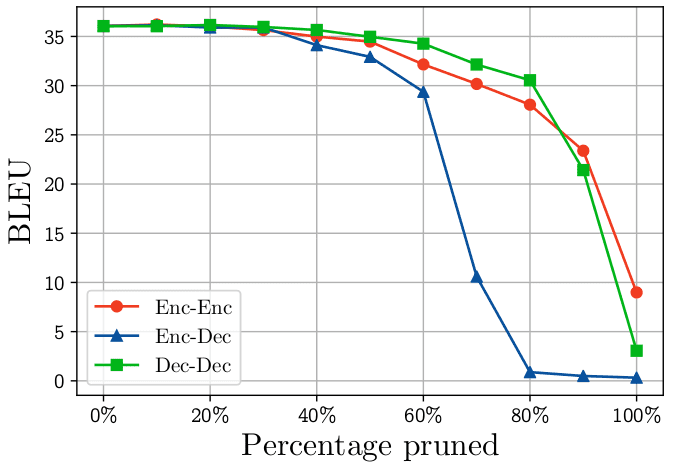
Michel et al. Supply: Are Sixteen Heads Actually Higher than One?

The authors present that pruning greater than 60% of the cross consideration heads of the vanilla transformer will lead to important efficiency degradation.

Perception 4: The encoder-decoder (cross) consideration is considerably extra depending on the multi-headed decomposed illustration.

After making use of softmax, self-attention is low rank

Lastly, there’s a work by Sinong Wang et al. [7] that implies that after making use of softmax, self-attention of all of the layers is of low rank.

Once more, the cumulative diagram depicts the sum of eigenvalues (in descending order for the X-axis). Broadly talking, if the normalized cumulative sums as much as 1 by utilizing only a few eigenvalues it implies that these are the vital dimensions.

For the plot, they utilized singular worth decomposition into P throughout layers and heads of the pretrained mannequin, and plot the normalized cumulative singular worth averaged over 10k sentences

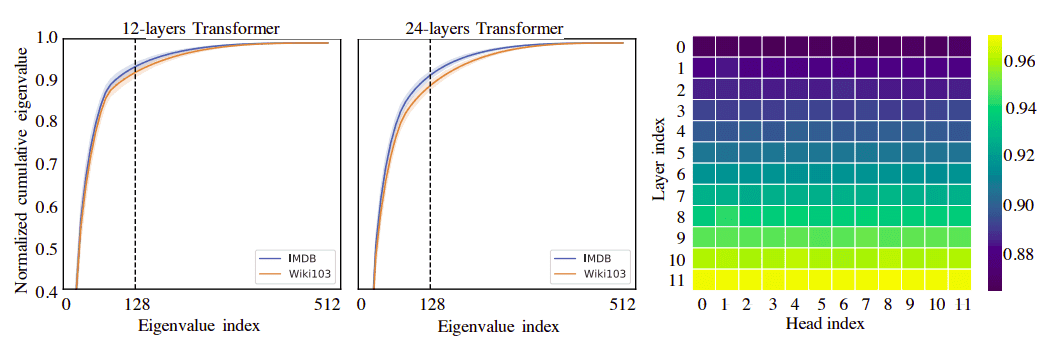
Supply: Linformer: Self-Consideration with Linear Complexity

Perception 5: After making use of softmax, (self) consideration is of low rank. This suggests that an ideal a part of the knowledge contained in $P$ will be recovered from the primary largest singular values (128 right here).

Based mostly on this statement, they proposed a easy linear consideration mechanism by down-projecting the keys and values, referred to as Linformer consideration.

Consideration weights as quick weight reminiscence Programs

Context-dependent quick weight technology was launched within the early 90s by Schmidhuber et al 1991. A gradual web with gradual weights regularly generates quick weights for a quick web, making the quick weights successfully depending on the context.

By eradicating the softmax within the well-known consideration mechanism we have now comparable conduct.

The place the outer product of values and keys will be thought to be the quick weights.

This is kind of the database, whereby:

Lastly, you get one thing that appears just like the quick weights described within the 90’:

Based mostly on this statement, they talk about a number of methods to substitute the removing of the softmax operations and make associations to already proposed linear-complexity consideration strategies. Right here is one perception that I appreciated from this work:

Perception 6: “As a consequence, to stop associations from interfering with one another upon retrieval, the respective keys must be orthogonal. In any other case, the dot product will attend to a couple of key and return a linear mixture of values.” Schlag et al.

Yannic Kilcher analyzes this paper extensively within the following video:

Rank collapse and token uniformity

Not too long ago, dong et al. [6] discovered that self-attention possesses an inductive bias in the direction of token uniformity.

Perception 7: Stunning the viewers, they seen that with out further parts resembling MLP and skip-connections, the eye converges exponentially to a rank-1 matrix.

To this finish, they studied mechanisms which can be accountable to counteract rank collapse. Briefly, they discovered the next:

1. Skip connections are essential: they stop the transformer output from degenerating to rank one exponentially shortly with respect to community depth.

2. Multi-layer perceptrons that venture the options in a better dimension and the again to the preliminary dimension additionally assist

3. Layer normalization performs no function in stopping rank collapse.

I’m betting that you just is perhaps questioning what Layer norm is beneficial for.

Layer norm: the important thing ingredient to switch studying largely pretrained transformers

To begin with, normalization strategies are the important thing to steady coaching and sooner convergence within the present dataset. Nevertheless, their trainable parameters pose sensible challenges for switch studying.

Within the transformer case, the paper “Pretrained Transformers As Common Computation Engines” [10] offers some insights on fine-tuning solely layer norm, which corresponds to the $gamma$ and $beta$ trainable parameters.

Intuitively, these parameters correspond to rescaling and shifting the eye sign.

They made big ablation research on essentially the most vital parts to be finetuned for datasets that belong to low-data regimes.

Perception 8: Surprisingly, the authors have discovered that the layer norm trainable parameters (0.1% of the parameters) to be essentially the most essential for fine-tuning transformers, after pretraining in big (excessive knowledge regime) pure language duties [10].

You may think about low-data regimes to domains the place getting big quantities of labeled knowledge is expensive and tough like medical imaging. Nevertheless, of their work, they use datasets resembling MNIST and CIFAR-10 as low-data regime datasets. And they’re in comparison with the massive quantity of texts {that a} transformer will be pretrained on.

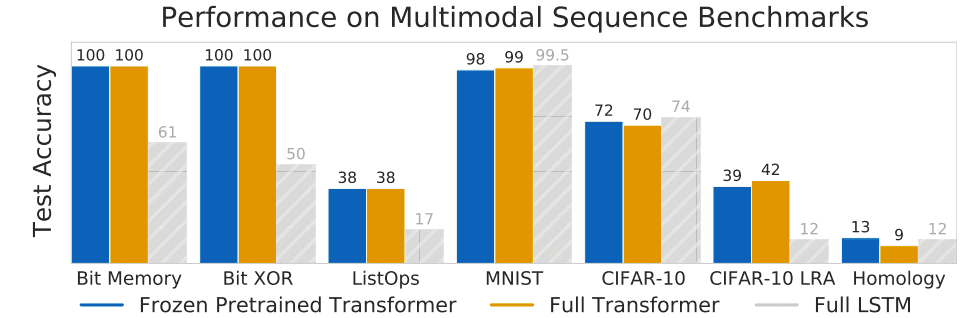
As it may be seen, the frozen transformer performs on par with the fully-fine-tuned transformer, which suggests two issues:

Perception 9: Pretraning self-attention on large pure language datasets leads to wonderful computational primitives.

Computation primitives are constructs or parts that are not damaged down (in a given context, resembling a programming language or an atomic aspect of an expression in language). In different phrases, primitives are the smallest models of processing. And because it seems, the discovered Q, Okay, V projection matrices in these massive NLP datasets discovered transferable primitives.

Perception 10: Nice-tuning the eye layers can result in efficiency divergence on small datasets.

On Quadratic Complexity: are we there but?

We can not conclude the eye mechanisms with out indicating the massive quantity of analysis spent on discovering alternate options for his or her quadratic complexity. I provides you with a brief glimpse of what’s taking place within the following picture from Yi Tay et al. 2020:

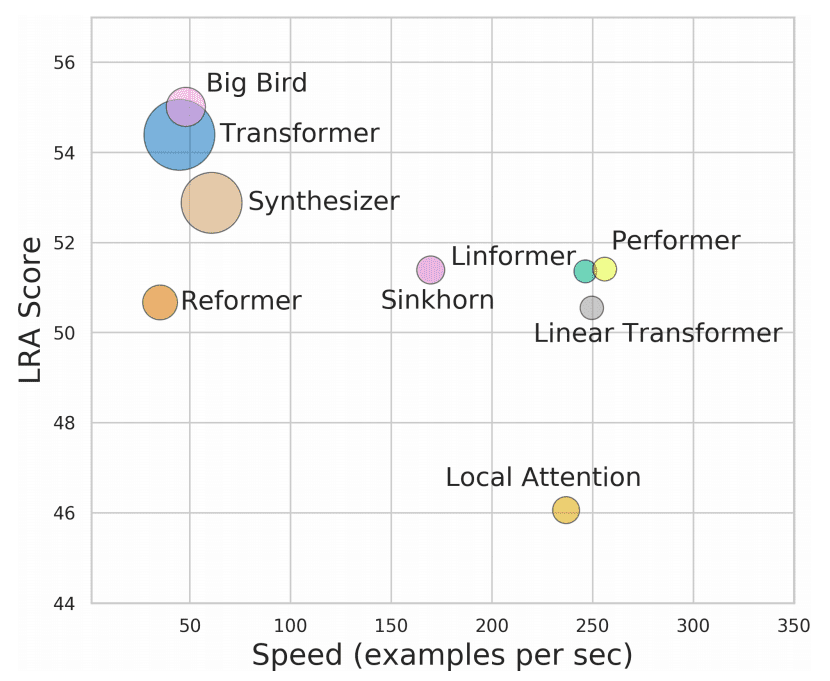
Supply: Lengthy Vary Area: A Benchmark for Environment friendly Transformers

Usually, there are two classes right here:

1. Strategies that use math to approximate the total quadratic international consideration (all2all), just like the Linformer that exploits matrix ranks.

2. Strategies that attempt to constrict and sparsify consideration. Probably the most primitive instance is “windowed” consideration which is conceptually just like convolutions (Determine (b) under). Probably the most profitable sparse-base methodology is Huge Fowl, as depicted under makes use of the mixture of the above consideration sorts.

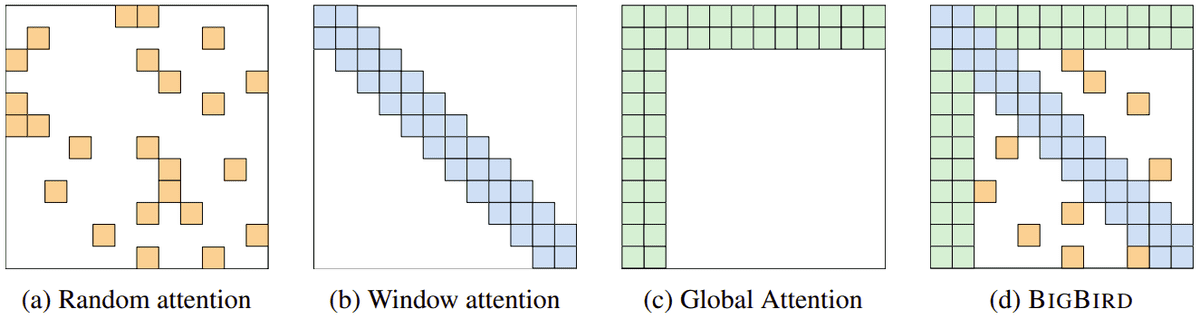
Supply: Huge Fowl: Transformers for Longer Sequences, by Zaheer et al.

Clearly, international consideration is saved for the “particular” tokens just like the CLS token that’s used for classification.

That being stated, the trail to decreasing the quadratic complexity is way from over.

I’m planning to supply a complete new article as soon as the sector turns into clear. Nonetheless, if you’re severe about operating some giant sparse consideration fashions test Deepspeed. It is likely one of the most well-known and quick implementations of sparse transformers, developed by Microsoft. It offers GPU implementations for Pytorch with large speedups.

Conclusion

After so many views and observations, I hope you gained no less than one new perception within the evaluation of content-based consideration. For my part, it’s superb how such a easy thought can have such immense impression and so many meanings and insights.

For those who appreciated this text share it on social media in order to succeed in extra curious folks with comparable questions. It could be extremely appreciated, I provide you with my phrase!

Acknowledgment

An enormous shout out to Yannic Kilcher for explaining so many movies about transformers and a focus. It’s unbelievable that his movies accelerated the training means of so many researchers across the globe.

References

[1] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Consideration is all you want. arXiv preprint arXiv:1706.03762.

[2] Michel, P., Levy, O., & Neubig, G. (2019). Are sixteen heads actually higher than one?. arXiv preprint arXiv:1905.10650.

[3] Cordonnier, J. B., Loukas, A., & Jaggi, M. (2020). Multi-Head Consideration: Collaborate As a substitute of Concatenate. arXiv preprint arXiv:2006.16362.

[4] Voita, E., Talbot, D., Moiseev, F., Sennrich, R., & Titov, I. (2019). Analyzing multi-head self-attention: Specialised heads do the heavy lifting, the remaining will be pruned. arXiv preprint arXiv:1905.09418.

[5] Schlag, I., Irie, Okay., & Schmidhuber, J. (2021). Linear Transformers Are Secretly Quick Weight Reminiscence Programs. arXiv preprint arXiv:2102.11174.

[6] Yihe Dong et al. 2021. Consideration will not be all you want: pure consideration loses rank doubly exponentially with depth

[7] Wang, S., Li, B., Khabsa, M., Fang, H., & Ma, H. (2020). Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768.

[8] Tay, Y., Dehghani, M., Abnar, S., Shen, Y., Bahri, D., Pham, P., … & Metzler, D. (2020). Lengthy Vary Area: A Benchmark for Environment friendly Transformers. arXiv preprint arXiv:2011.04006.

[9] Zaheer, M., Guruganesh, G., Dubey, A., Ainslie, J., Alberti, C., Ontanon, S., … & Ahmed, A. (2020). Huge hen: Transformers for longer sequences. arXiv preprint arXiv:2007.14062.

[10] Lu, Okay., Grover, A., Abbeel, P., & Mordatch, I. (2021). Pretrained Transformers as Common Computation Engines. arXiv preprint arXiv:2103.05247.

* Disclosure: Please word that a few of the hyperlinks above is perhaps affiliate hyperlinks, and at no further price to you, we are going to earn a fee for those who determine to make a purchase order after clicking by means of.