If you’re a machine studying researcher/engineer these days it’s best to undoubtedly concentrate on einsum operations!
Personally talking, I used to surrender understanding git repos due to einsum operations. The explanation: regardless that I felt fairly comfy with tensor operations einsum was not in my arsenal.
Lengthy story quick, I made a decision I wish to get conversant in the einsum notation. Since I’m notably focused on transformers and self-attention in laptop imaginative and prescient, I’ve an enormous playground.
On this article, I’ll extensively attempt to familiarize myself with einsum (in Pytorch), and in parallel, I’ll implement the well-known self-attention layer, and at last a vanilla Transformer.
The code is completely academic! I haven’t skilled any massive self-attention mannequin but however I plan to. Honestly talking, I discovered far more within the course of than I initially anticipated.
If you wish to delve into the idea first, be happy to examine my articles on consideration and transformer.
If not, let the sport start!
The code of this tutorial is offered on GitHub. Present your help with a star!
Why einsum?
First, einsum notation is all about elegant and clear code. Many AI trade specialists and researchers use it constantly:
To persuade you much more, let’s see an instance:
You wish to merge 2 dims of a 4D tensor, first and final.
x = x.permute(0, 3, 1, 2)
N, W, C, H = x.form
x = x.contiguous().view(N * W, C, -1)
This isn’t the optimum option to code it, however it serves my level!
Personally, this code freaks me out!
It’s an excellent observe to enhance your code’s readability with einsum. Within the earlier case that may be one thing like this:
x = einops.rearrange(x, 'b c h w -> (b w) c h')
Neat and clear!
Second cause: if you happen to care about batched implementations of customized layers with multi-dimensional tensors, einsum ought to undoubtedly be in your arsenal!
Third cause: translating code from PyTorch to TensorFlow or NumPy turns into trivial.
I’m utterly conscious that it takes time to get used to it. That’s why I made a decision to implement some self-attention mechanisms.
The einsum and einops notation fundamentals
If you already know the fundamentals of einsum and einops you could skip this part.
Einsum
To cope with multi-dimensional computations again in 1916 Albert Einstein developed a compact kind to point summation over some indexes. The so-called Einstein summation conference is what we use once we name einsum.
In a nutshell, that is how einsum instructions are structured:
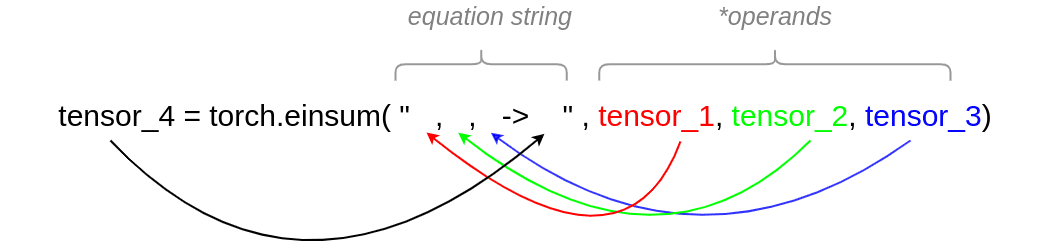
Picture by Writer
We will cut up the arguments of einsum into two elements:
Equation string: Right here is the place all of the indices will likely be. Every index will point out the dimension of the tensor. To do this, we use lowercase letters. For operations that will likely be carried out on an axis of equal dimension on a number of tensors, we should use the identical image. This supplies einsum with the data that we’ll carry out fancy stuff on this dimension. There should be as many commas on the left aspect of -> because the tensor that we use. I consider that the coloured arrows make that clear.
On the suitable aspect of -> now we have the index of the output of the operation we carry out. We want as many indexes because the output dimensions. The letters (indices) that we use on the output should exist on the suitable aspect of the equation string.
Operands: We will present as many tensors as we wish. Clearly, the variety of tensors should be exactly the identical because the left a part of the -> equation.
An instance: Batch Matrix Multiplication with einsum
Let’s say now we have 2 tensors with the next shapes and we wish to carry out a batch matrix multiplication in Pytorch:
a = torch.randn(10,20,30)
c = torch.randn(10,50,30)
With einsum you possibly can clearly state it with one elegant command:
y1 = torch.einsum('b i ok, b j ok -> b i j', a , c)
Let’s divide the method of writing the command into steps:
-
We place out tensors within the second argument as operands
-
We put a string with the -> image
-
Left to the -> image: Since now we have two tensors a, c now we have to index their dimensions. Each have 3 dims so now we have to make use of symbols for every one of many three dimensions (6 in complete). I take advantage of the identical image b for the batch dim (5 in complete). Let’s make them 4 (see beneath why): b, i, ok for tensor a and b, j, ok for tensor c
-
For the axes that will likely be summed as a consequence of matrix multiplication, now we have to make use of the identical image to index each a and c. In that case that would be the index ok (4 symbols). That may clarify to einsum that that is the axis that we wish to function on.
-
Proper to the -> image: The ensuing dimensions primarily based on the operation. We have now to make use of the earlier symbols right here. This may point out the form of the consequence and einsum will perceive that it’s a multiplication.
With out einsum, you would need to permute the axes of b and after apply batch matrix multiplication. You even have to recollect the command of Pytorch for batch matrix multiplication.
y2 = torch.bmm(a, c.permute(0, 2, 1))
Let’s use the einsum notation to shortly function on a single tensor.
Einops
Although einops is a normal library, right here I’ll solely cowl einops.rearrange. It’s been proved extraordinarily helpful to me up to now.
In einops, the equation string is strictly the identical. The argument order is reversed. You specify the tensor or the checklist of tensors first. The next picture could make clear issues out:

Picture by creator
The underscores are for illustration functions solely. We’d put symbols in an actual instance. You possibly can perceive from the variety of underscores, that this operation will merge a number of the two dimensions collectively (composition). On the left a part of the equation string, now we have the 4 enter dimensions and on the suitable, solely three are remaining.
With einsum, as a substitute, that may most likely imply summation over one axis.
In case a listing of tensors is supplied in rearrange, the primary dimension (depicted as underscore) will seek advice from the size of the checklist, which is the variety of tensors
I additionally adore the decomposition flexibility of einops. It’s an awesome illustration of the axes’ size additionally! Right here is an instance:
qkv = torch.rand(2,128,3*512)
q, ok, v = tuple(rearrange( qkv , 'b t (d n) -> n b t d ', n=3))
We cut up – decompose – the axis in 3 equal elements! Notice that to be able to decompose an axis you could specify the size of the index/axis.
The tuple command will use the primary tensor’s dimension and it’ll create a tuple of n=3 tensors.
Conference: All through this text, I extensively use einops.rearrange after I function on a single tensor and torch.einsum after I function on a number of tensors.
Axis indexing guidelines
The distinction with einops is that you need to use greater than single lowercase letters for indexing a dimension (i.e flattening a 2D tensor: “nikolas , aisummer -> (nikolas aisummer) ’’).
Nonetheless, you at all times want to depart some area between the indices of the axis on this manner. For comfort, I’ll depart an area in torch.einsum operations additionally and I’ll attempt to use single letters for indexing.
Lastly, if you happen to really feel you want extra observe with einsum and einops, advise the acknowledgments part.
Now let’s write some code!
After some considering, I spotted that one of the simplest ways to know the implementations is to interrupt it down into steps with some math. I additionally point out the steps within the code.
Scaled dot product self-attention
The mathematics in steps
Step 1: Create linear projections, given enter . The matrix multiplication occurs within the dimension. For NLP, that may be the dimensionality of phrase embeddings.
to_qvk = nn.Linear(dim, dim * 3, bias=False)
qkv = to_qvk(x)
q, ok, v = tuple(rearrange(qkv, 'b t (d ok) -> ok b t d ', ok=3))
Step 2: Calculate scaled dot product, apply masks, and at last compute softmax in (final) dimension
scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, ok) * self.scale_factor
if masks is not None:
assert masks.form == scaled_dot_prod.form[1:]
scaled_dot_prod = scaled_dot_prod.masked_fill(masks, -np.inf)
consideration = torch.softmax(scaled_dot_prod, dim=-1)
Step 3: Multiply scores with
torch.einsum('b i j , b j d -> b i d', consideration, v)
Implementation of scaled dot product self-attention
import numpy as np
import torch
from einops import rearrange
from torch import nn
class SelfAttentionAISummer(nn.Module):
"""
Implementation of plain self consideration mechanism with einsum operations
Paper: https://arxiv.org/abs/1706.03762
Weblog: https://theaisummer.com/transformer/
"""
def __init__(self, dim):
"""
Args:
dim: for NLP it's the dimension of the embedding vector
the final dimension dimension that will likely be supplied in ahead(x),
the place x is a 3D tensor
"""
tremendous().__init__()
self.to_qvk = nn.Linear(dim, dim * 3, bias=False)
self.scale_factor = dim ** -0.5
def ahead(self, x, masks=None):
assert x.dim() == 3, '3D tensor should be supplied'
qkv = self.to_qvk(x)
q, ok, v = tuple(rearrange(qkv, 'b t (d ok) -> ok b t d ', ok=3))
scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, ok) * self.scale_factor
if masks is not None:
assert masks.form == scaled_dot_prod.form[1:]
scaled_dot_prod = scaled_dot_prod.masked_fill(masks, -np.inf)
consideration = torch.softmax(scaled_dot_prod, dim=-1)
return torch.einsum('b i j , b j d -> b i d', consideration, v)
Code clarification
It is very important discover the softmax dimension. Right here we used the final one. Nonetheless, the scaled dot product is a sq. matrix for every enter sequence (tokens x tokens). Somebody would argue that we might use the opposite dimension.
The reply is straightforward: you must multiply within the dimension you apply the softmax. Watch out of that.
One other factor is that we used a single linear layer for the linear projections. That is completely okay because it’s the identical operation utilized 3 instances. We then need to decompose the illustration by casting it to q,v,ok.
Multi-Head Self-Consideration
Let’s see how we are able to introduce a number of heads in our computations. This kind of consideration is named Multi-Head Self-Consideration (MHSA). Intuitively we’ll carry out a number of computations in a lower-dimensional area (dim_head within the code). The a number of computations are utterly impartial. It’s conceptually just like batch dimension. You possibly can consider it as a batch of low-dimensional self-attentions.
For my part, that is the place the expressive energy of the einsum notation will shock you.
The code in steps
Step 1: Create linear projections per head. The matrix multiplication occurs within the dimension. As an alternative of , now we’ll challenge into outputs.
The heads have decrease dimensionality , and truly it is not uncommon to make use of .
to_qvk = nn.Linear(dim, dim_head * heads * 3, bias=False)
qkv = self.to_qvk(x)
Step 2: Decompose representations per head.
q, ok, v = tuple(rearrange(qkv, 'b t (d ok h) -> ok b h t d ', ok=3, h=self.heads))
Step 3: Calculate scaled dot product, apply the masks, and at last compute softmax in – final dimension. Principally, we simply have yet another dimension that corresponds to the variety of heads. The computation is carried out precisely the identical manner.
scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, ok) * self.scale_factor
if masks is not None:
assert masks.form == scaled_dot_prod.form[2:]
scaled_dot_prod = scaled_dot_prod.masked_fill(masks, -np.inf)
consideration = torch.softmax(scaled_dot_prod, dim=-1)
Step 4: Multiply per head dot product scores with
out = torch.einsum('b h i j , b h j d -> b h i d', consideration, v)
Step 5: Recompose/merge heads (h) with (the dimension of the computations up to now)
out = rearrange(out, "b h t d -> b t (h d)")
Step 6: Apply remaining linear transformation layer
self.W_0 = nn.Linear( _dim, dim, bias=False)
self.W_0(out)
Implementation of MHSA
import numpy as np
import torch
from einops import rearrange
from torch import nn
class MultiHeadSelfAttentionAISummer(nn.Module):
def __init__(self, dim, heads=8, dim_head=None):
"""
Implementation of multi-head consideration layer of the unique transformer mannequin.
einsum and einops.rearrange is used every time attainable
Args:
dim: token's dimension, i.e. phrase embedding vector dimension
heads: the variety of distinct representations to be taught
dim_head: the dim of the top. Basically dim_head<dim.
Nonetheless, it could not essential be (dim/heads)
"""
tremendous().__init__()
self.dim_head = (int(dim / heads)) if dim_head is None else dim_head
_dim = self.dim_head * heads
self.heads = heads
self.to_qvk = nn.Linear(dim, _dim * 3, bias=False)
self.W_0 = nn.Linear( _dim, dim, bias=False)
self.scale_factor = self.dim_head ** -0.5
def ahead(self, x, masks=None):
assert x.dim() == 3
qkv = self.to_qvk(x)
q, ok, v = tuple(rearrange(qkv, 'b t (d ok h) -> ok b h t d ', ok=3, h=self.heads))
scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, ok) * self.scale_factor
if masks is not None:
assert masks.form == scaled_dot_prod.form[2:]
scaled_dot_prod = scaled_dot_prod.masked_fill(masks, -np.inf)
consideration = torch.softmax(scaled_dot_prod, dim=-1)
out = torch.einsum('b h i j , b h j d -> b h i d', consideration, v)
out = rearrange(out, "b h t d -> b t (h d)")
return self.W_0(out)
TransformerEncoder
In case you forgot, the vanilla transformer seems like this:
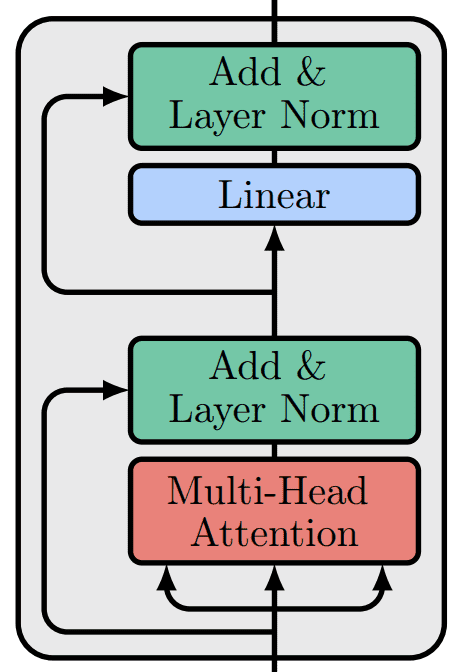
Picture by Writer primarily based on the code of
Renato Negrinho
Having a strong code for MHSA, constructing a Transformer block is as simple as this:
from torch import nn
from .mhsa import MultiHeadSelfAttention
class TransformerBlockAISummer(nn.Module):
"""
Vanilla transformer block from the unique paper "Consideration is all you want"
Detailed evaluation: https://theaisummer.com/transformer/
"""
def __init__(self, dim, heads=8, dim_head=None, dim_linear_block=1024, dropout=0.1):
"""
Args:
dim: token's vector size
heads: variety of heads
dim_head: if none dim/heads is used
dim_linear_block: the inside projection dim
dropout: chance of droppping values
"""
tremendous().__init__()
self.mhsa = MultiHeadSelfAttention(dim=dim, heads=heads, dim_head=dim_head)
self.drop = nn.Dropout(dropout)
self.norm_1 = nn.LayerNorm(dim)
self.norm_2 = nn.LayerNorm(dim)
self.linear = nn.Sequential(
nn.Linear(dim, dim_linear_block),
nn.ReLU(),
nn.Dropout(dropout),
nn.Linear(dim_linear_block, dim),
nn.Dropout(dropout)
)
def ahead(self, x, masks=None):
y = self.norm_1(self.drop(self.mhsa(x, masks)) + x)
return self.norm_2(self.linear(y) + y)
Since now we have extensively coated this structure, I’ll allow you to analyze the code your self.
Lastly, we are able to stack a number of such blocks collectively and create our fancy Transformer Encoder:
class TransformerEncoderAISummer(nn.Module):
def __init__(self, dim, blocks=6, heads=8, dim_head=None):
tremendous().__init__()
self.block_list = [TransformerBlock(dim, heads, dim_head) for _ in range(blocks)]
self.layers = nn.ModuleList(self.block_list)
def ahead(self, x, masks=None):
for layer in self.layers:
x = layer(x, masks)
return x
Homework: construct the Imaginative and prescient Transformer 🙂
Conclusion
It took me a while to solidify my understanding of self-attention and einsum, however it was a enjoyable trip. Within the subsequent article, I’ll attempt to implement extra superior self-attention blocks for laptop imaginative and prescient. In the meantime, use our Github repository in your subsequent challenge and tell us the way it goes out.
Don’t overlook to star our repository to indicate us your help!
If you happen to really feel like your PyTorch fundamentals want some further observe, be taught from the most effective ones on the market. Use the code aisummer35 to get an unique 35% low cost out of your favorite AI weblog 🙂
Acknowledgments
An enormous shout out to Alex Rogozhnikov (@arogozhnikov) for the superior einops lib.
Here’s a checklist of different sources that considerably accelerated my studying on einsum operations, consideration, or transformers:
* Disclosure: Please observe that a number of the hyperlinks above could be affiliate hyperlinks, and at no further value to you, we’ll earn a fee if you happen to resolve to make a purchase order after clicking by way of.
