Intuitive Explanation of Skip Connections in Deep Learning

These days, there may be an infinite variety of purposes that somebody can do with Deep Studying. Nevertheless, in an effort to perceive the plethora of design selections resembling skip connections that you just see in so many works, it’s crucial to grasp a bit of little bit of the mechanisms of backpropagation.

Should you have been attempting to coach a neural community again in 2014, you’ll undoubtedly observe the so-called vanishing gradient downside. In easy phrases: you’re behind the display checking the coaching technique of your community and all you see is that the coaching loss cease lowering however it’s nonetheless far-off from the specified worth. You examine all of your code strains to see if one thing was unsuitable all night time and you discover no clue. Not the perfect expertise on the planet, consider me!

The replace rule and the vanishing gradient downside

So, let’s remind our self’s the replace rule of gradient descent with out momentum, given L to be the loss perform and $lambda$ the educational charge:

w_{i}’ = w_{i} + Delta w_{i}

the place $Delta w_{i} = – lambda frac{partial L}{partial Delta w_{i}}$

What’s principally taking place is that you just attempt to replace the parameters by altering them with a small quantity $Delta w_{i}$

Trying a bit of bit within the concept, one can simply grasp the vanishing gradient downside from the backpropagation algorithm. We will briefly examine the backpropagation algorithm from the prism of the chain rule, ranging from fundamental calculus to achieve an perception on skip connections.

Briefly, backpropagation is the “optimization-magic” behind deep studying architectures. Given {that a} deep community consists of a finite variety of parameters that we wish to be taught, our objective is to iteratively optimize these parameters with respect to the loss perform L.

As you’ve got seen, every structure has some enter (i.e. a picture) and produces an output (prediction). The loss perform is closely primarily based on the duty we wish to clear up. For now, what you have to know is the loss perform is a quantitative measure of the space between two tensors, that may characterize a picture label, a bounding field in a picture, a translated textual content in one other language and so on. You normally want some form of supervision to check the community’s prediction with the specified consequence (floor reality). Understand that backpropagation belongs within the supervised machine studying class.

So, the attractive thought of backpropagation is to regularly reduce this loss by updating the parameters of the community. However how are you able to propagate the scalar measured loss inside the community? That’s precisely the place backpropagation comes into play.

Backpropagation and partial derivatives

In easy phrases, backpropagation is about understanding how altering the weights (parameters) in a community modifications the loss perform by computing the partial derivatives. For the latter, we use the easy thought of the chain rule, to reduce the space within the desired predictions. In different phrases, backpropagation is all about calculating the gradient of the loss perform whereas contemplating the totally different weights inside that neural community, which is nothing greater than calculating the partial derivatives of the loss perform with respect to mannequin parameters. By repeating this step many occasions, we’ll regularly reduce the loss perform till it stops decreasing, or another predefined termination standards are met.

Chain rule

The chain rule principally describes the gradient (change) of a loss perform i.e. z with respect to some neural community parameter, let’s
say x and y that are features of a earlier layer parameter t. Let
f, g, h be totally different layers on the community that carry out a non-linear operation
within the enter vector.

z = f(x,y) quad x = g(t) quad y = h(t)

Now, suppose that you’re studying calculus and also you wish to specific the gradient
of z with respect to the enter. That is what you be taught in multi-variable calculus:

frac{partial z}{partial t } = frac{partial f}{partial x} frac{partial x}{partial t} + frac{partial f}{partial y} frac{partial y}{partial t}

Apparently, the well-known algorithm does precisely the identical operation however within the reverse method: it begins from the output z and calculates the partial derivatives of every parameter, expressing it solely primarily based on the gradients of the later layers.

It’s actually value noticing that all these values are sometimes lower than 1, impartial of the signal. To be able to propagate the gradient to the sooner
layer’s, backpropagation makes use of multiplication of the partial derivatives (as within the chain rule). On the whole, multiplication with absolute worth lower than 1 is good as a result of it offers some sense of coaching stability, though there may be not a strict mathematic theorem about that. Nevertheless, one can observe that for each layer that we go backwards within the community the gradient of the community will get smaller and smaller.

Skip connections for the win

At current, skip connection is an ordinary module in lots of convolutional architectures. By utilizing a skip connection, we offer an alternate path for the gradient (with backpropagation). It’s experimentally validated that this extra paths are sometimes useful for the mannequin convergence. Skip connections in deep architectures, because the identify suggests, skip some layer within the neural community and
feeds the output of 1 layer because the enter to the following layers (as an alternative of solely the following one).

As beforehand defined, utilizing the chain rule, we should maintain multiplying phrases with the error gradient as we go backwards. Nevertheless, within the lengthy chain of
multiplication, if we multiply many issues collectively which can be lower than one, then the ensuing gradient can be very small. Thus, the gradient turns into very small as we method the sooner layers in a deep structure. In some instances, the gradient turns into zero, that means that we don’t replace the early layers in any respect.

On the whole, there are two basic ways in which one may use skip connections via totally different non-sequential layers:

a) addition as in residual architectures,

b) concatenation as in densely related architectures.

We’ll first describe addition which is usually referred as residual skip connections.

ResNet: skip connections through addition

The core thought is to backpropagate via the id perform, by simply utilizing a vector addition. Then the gradient would merely be multiplied by one and its worth can be maintained within the earlier layers. That is the major thought behind Residual Networks (ResNets): they stack these skip residual blocks collectively. We use an id perform to protect the gradient.

Picture is taken from Res-Web unique paper

Mathematically, we are able to characterize the residual block, and calculate its partial spinoff (gradient), given the loss perform like this:

frac{partial L}{partial x } = frac{partial L}{partial H} frac{partial H}{partial x} = frac{partial L}{partial H} ( frac{partial F}{partial x} + 1 ) = frac{partial L}{partial H} frac{partial F}{partial x} + frac{partial L}{partial H}

Aside from the vanishing gradients, there may be another excuse that we generally use them. For a plethora of duties (resembling semantic segmentation, optical stream estimation , and so on.) there may be some data that was captured within the preliminary layers and we want to enable the later layers to additionally be taught from them. It has been noticed that in earlier layers the realized options correspond to decrease semantic data that’s extracted from the enter. If we had not used the skip connection that data would have turned too summary.

DenseNet: skip connections through concatenation

As said, for a lot of dense prediction issues, there may be low-level data shared between the enter and output, and it might be fascinating to cross this data straight throughout the online. The choice method that you may obtain skip connections is by concatenation of earlier characteristic maps. Essentially the most well-known deep studying structure is DenseNet. Under you’ll be able to see an instance of characteristic resusability by concatenation with 5 convolutional layers:

densenet-architecture-skip-connections

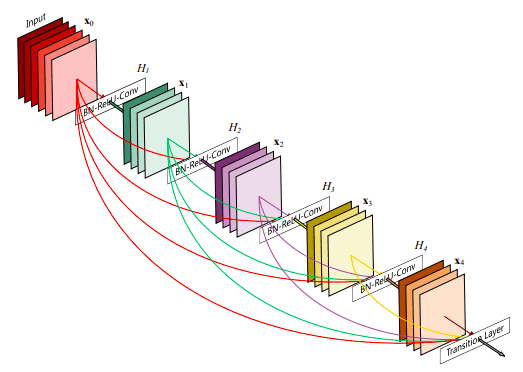
Picture is taken from DenseNet unique paper

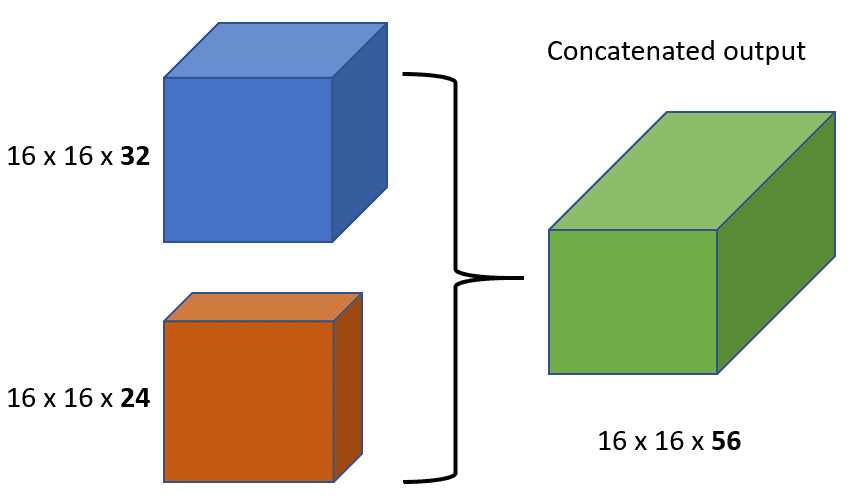
This structure closely makes use of characteristic concatenation in order to make sure most data stream between layers within the community. That is achieved by connecting through concatenation all layers straight with one another, versus ResNets. Virtually, what you principally do is to concatenate the characteristic channel dimension. This results in

a) an monumental quantity of characteristic channels on the final layers of the community,

b) to extra compact fashions, and

c) excessive characteristic reusability.

resnet-concatenation

Quick and Lengthy skip connections in Deep Studying

In additional sensible phrases, you must watch out when introducing additive skip connections in your deep studying mannequin. The dimensionality needs to be the identical as well as and in addition in concatenation aside from the chosen channel dimension. That’s the reason why you see that additive skip connections are utilized in two sorts of setups:

a) brief skip connections

b) lengthy skip connections.

Quick skip connections are used together with consecutive convolutional layers that don’t change the enter dimension (see Res-Web), whereas lengthy skip connections normally exist in encoder-decoder architectures. It’s identified that the world data (form of the picture and different statistics) resolves what, whereas native data resolves the place (small particulars in a picture patch).

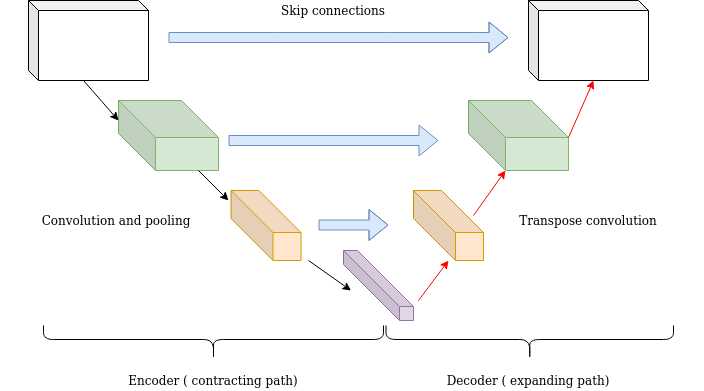
Lengthy skip connections usually exist in architectures which can be symmetrical, the place the spatial dimensionality is decreased within the encoder half and is regularly elevated within the decoder half as illustrated beneath. Within the decoder half, one can enhance the dimensionality of a characteristic map through transpose convolutional layers. The transposed convolution operation varieties the identical connectivity as the conventional convolution however within the backward course.

U-Nets: lengthy skip connections

Mathematically, if we specific convolution as a matrix multiplication, then transpose convolution is the reverse order multiplication (BxA as an alternative
of AxB). The aforementioned structure of the encoder-decoder scheme together with lengthy skip connections is commonly referred as U-shape (Unet). It’s
utilized for duties that the prediction has the identical spatial dimension because the enter resembling picture segmentation, optical stream estimation, video prediction, and so on.

Lengthy skip connections might be fashioned in a symmetrical method, as proven within the diagram beneath:

long-skip-connection

By introducing skip connections within the encoder-decoded structure, fine-grained particulars might be recovered within the prediction. Even
although there isn’t a theoretical justification, symmetrical lengthy skip connections work extremely successfully in dense prediction duties (medical picture segmentation).

Conclusion

To sum up, the motivation behind this kind of skip connections is that they’ve an uninterrupted gradient stream from the primary layer to the final layer, which tackles the vanishing gradient downside. Concatenative skip connections allow an alternate method to make sure characteristic reusability of the identical dimensionality from the sooner layers and are extensively used.

Alternatively, lengthy skip connections are used to cross options from the encoder path to the decoder path in an effort to recuperate spatial data misplaced throughout downsampling. Quick skip connections seem to stabilize gradient updates in deep architectures. Lastly, skip connections allow characteristic reusability and stabilize coaching and convergence.

As a ultimate be aware, encouraging additional studying , it has been experimentally validated Li et al 2018 the the loss panorama modifications considerably when introducing skip connections, as illustrated beneath:

skip-connections-visualizing-landscape

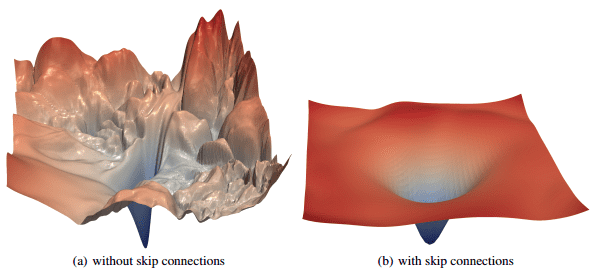
Picture is taken from this paper

Should you want extra details about Skip Connections and Convolutional Neural Networks, the Convolutional Neural Community Course on-line course by Andrew Ng and Coursera is your best choice. It’s a very complete materials with detailed explanations on how the fashions are utilized in real-world purposes, and it’ll cowl the whole lot you need. Moreover, it has a 4.9/5 score. That has to imply one thing.

Cited as:

@article{adaloglou2020skip,
    title   = "Intuitive Rationalization of Skip Connections in Deep Studying",
    writer  = "Adaloglou, Nikolas",
    journal = "https://theaisummer.com/",
    12 months    = "2020",
    url     = "https://theaisummer.com/skip-connections/"
  }

References

Çiçek, Ö., Abdulkadir, A., Lienkamp, S. S., Brox, T., & Ronneberger, O. (2016, October). 3D U-Web: studying dense volumetric segmentation from sparse annotation. In Worldwide convention on medical picture computing and computer-assisted intervention (pp. 424-432). Springer, Cham.
Ronneberger, O., Fischer, P., & Brox, T. (2015, October). U-net: Convolutional networks for biomedical picture segmentation. In Worldwide Convention on Medical picture computing and computer-assisted intervention (pp. 234-241). Springer, Cham.
He, Okay., Zhang, X., Ren, S., & Solar, J. (2016). Deep residual studying for picture recognition. In Proceedings of the IEEE convention on laptop imaginative and prescient and sample recognition (pp. 770-778).
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Studying representations by back-propagating errors. nature, 323(6088), 533-536.
Nielsen, M. A. (2015). Neural networks and deep studying (Vol. 2018). San Francisco, CA, USA:: Willpower press.
Huang, G., Liu, Z., Van Der Maaten, L., & Weinberger, Okay. Q. (2017). Densely related convolutional networks. In Proceedings of the IEEE convention on laptop imaginative and prescient and sample recognition (pp. 4700-4708).
Drozdzal, M., Vorontsov, E., Chartrand, G., Kadoury, S., & Pal, C. (2016). The significance of skip connections in biomedical picture segmentation. In Deep Studying and Information Labeling for Medical Purposes (pp. 179-187). Springer, Cham.
Li, H., Xu, Z., Taylor, G., Studer, C., & Goldstein, T. (2018). Visualizing the loss panorama of neural nets. In Advances in Neural Data Processing Programs (pp. 6389-6399).

* Disclosure: Please be aware that a number of the hyperlinks above is likely to be affiliate hyperlinks, and at no extra price to you, we’ll earn a fee if you happen to resolve to make a purchase order after clicking via.