Recurrent neural networks: building a custom LSTM cell

An infinite quantity of instances I’ve discovered myself in determined conditions as a result of I had no concept what was occurring beneath the hood. And, for lots of people within the pc imaginative and prescient group, recurrent neural networks (RNNs) are like this. Kind of, one other black field within the pile.

Nevertheless, on this tutorial, we are going to try and open the RNN magic black field and unravel its mysteries!

Despite the fact that I’ve come throughout a whole lot of tutorials on LSTM’s on the market, I felt there was one thing lacking. Due to this fact, I actually hope that this tutorial serves as a contemporary information to RNNs. We attempt to cope with a number of particulars of sensible nature. To this finish, we will construct upon their elementary ideas.

The huge utility subject of RNN’s consists of sequence prediction, exercise recognition, video classification in addition to a wide range of pure language processing duties. After a cautious inspection of the equations, we are going to construct our personal LSTM cell to validate our understanding. Lastly, we are going to make some associations with convolutional neural networks to maximise our comprehension. Accompanying code for this tutorial might be discovered right here.

It’s true that by the second you begin to examine RNN’s, particularly with a pc imaginative and prescient background, ideas misleadings begin to come up. Much less actually:

“Backpropagation with stochastic gradient descent (SGD) doesn’t magically make your community work. Batch normalization doesn’t magically make it converge sooner. Recurrent Neural Networks (RNNs) don’t magically allow you to “plug in” sequences. (…) When you insist on utilizing the know-how with out understanding the way it works you might be more likely to fail.” ~ Andrey Karpathy (Director of AI at Tesla)

The abstraction of RNN’s implementations does not enable customers to grasp how we cope with the time dimension in sequences! Nevertheless, by understanding the way it works you possibly can write optimized code and apply extensibility, in a method that you simply weren’t assured sufficient to do earlier than.

Lastly, a extra holistic strategy in RNN’s might be discovered on Sequence fashions from the Deep Studying specialization course supplied by Coursera.

A easy RNN cell

Recurrent cells are neural networks (often small) for processing sequential knowledge. As we already know, convolutional layers are specialised for processing grid-structured values (i.e. pictures). Quite the opposite, recurrent layers are designed for processing lengthy sequences, with none further sequence-based design selection [1].

One can obtain this by connecting the timesteps’ output to the enter! That is referred to as sequence unrolling. By processing the entire sequence, we’ve got an algorithm that takes under consideration the earlier states of the sequence. On this method, we’ve got the first notion of reminiscence (a cell)! Let’s take a look at it:

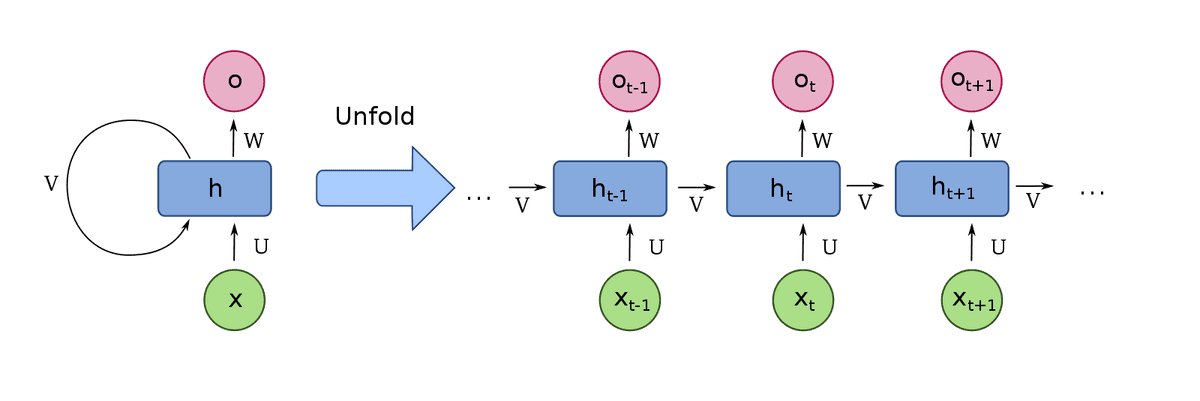
Visualization is borrowed from Wiki

Nearly all of widespread recurrent cells may also course of sequences of variable size. That is actually vital for a lot of purposes equivalent to movies, that comprise a distinct variety of pictures. One can view the RNN cell as a standard neural community with shared weights for the a number of timesteps. With this modification, the weights of the cell now have entry to the earlier states of the sequence.

However how can we probably prepare such sequential fashions?

What’s Again-propagation by time?

Most practitioners with pc imaginative and prescient background have little concept of what recurrency means. And it’s certainly obscure. As a result of the frameworks assume that you simply already know the way it works. Nevertheless, if you wish to discover an environment friendly resolution to your downside, it’s best to fastidiously design your structure based mostly on the issue.

The magic of RNN networks that no person sees is the enter unrolling. The latter signifies that given a sequence of size N, you course of the enter into timesteps.

We select to mannequin the time dimension with RNN’s, as a result of we need to study temporal and sometimes long-term dependencies.

Proper now, it’s true that convolutions can not deal with as a result of they’ve a finite receptive subject. Observe that, in principle, you possibly can apply a recurrent mannequin in any dimension.

When it comes to coaching an RNN mannequin, the problem is that now we’ve got a time-sequence. That’s why enter unrolling is the one method we are able to make backpropagation work!

So, how will you study a time-sequence? Ideally, we wish the reminiscence (parameters) of the cells to have taken under consideration all of the enter sequences. In any other case, we’d not have the ability to study the specified mapping. In essence, backpropagation requires a separate layer for every time step with the identical weights for all layers (enter unrolling)! The next picture helps to grasp this difficult concept.

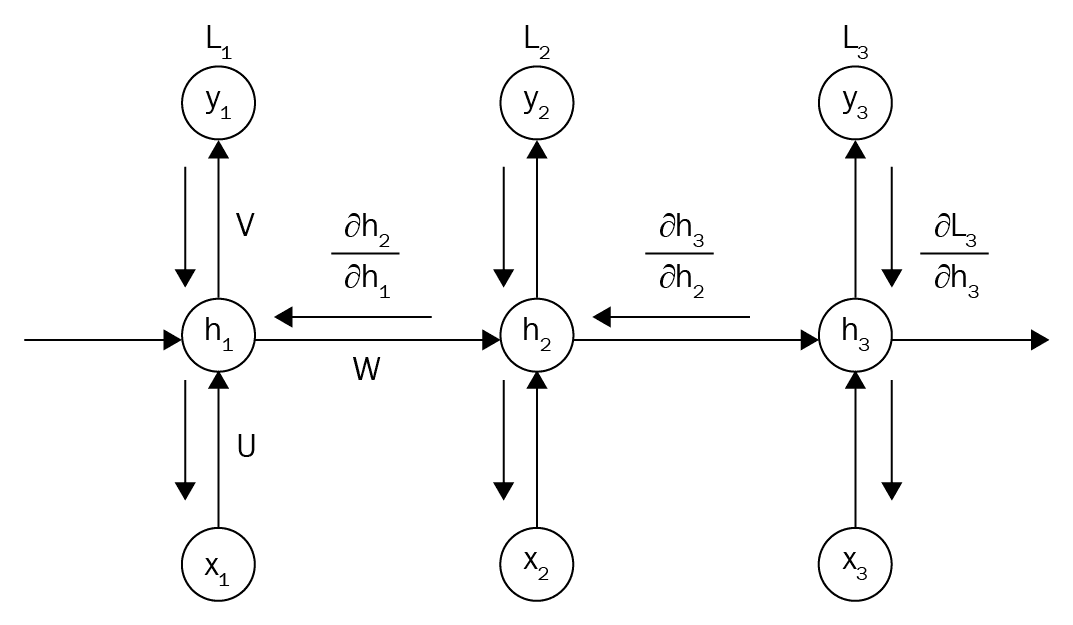
Supply: O’Reilly: hands-on-reinforcement-learning](Supply: O’Reilly: hands-on-reinforcement-learning)

Backpropagation by time was created based mostly on the pre-described statement. So, based mostly on the chunked (unrolled) enter, we are able to calculate a distinct loss per timestep. Then, we are able to backpropagate the error of a number of losses to the reminiscence cells. On this route, one can compute the gradients from a number of paths (timesteps) that then are added to calculate the ultimate gradient. Because of this, we might use totally different optimizers or normalization strategies in recurrent architectures.

In different phrases, we characterize the RNN as a repeated (feedforward) community. Extra importantly, the time and house complexity to provide the output of the RNN is asymptotically linear to the enter size (timesteps). This sensible bottleneck introduces the computational restrict of coaching actually giant sequences.

In truth, an analogous concept is applied in apply when you will have a small GPU and also you need to prepare your mannequin with an even bigger batch dimension than your reminiscence helps. You carry out ahead propagation with the primary batch and calculate the loss. Afterwards, you repeat the identical factor with the second batch and common the losses from totally different batches. On this method, gradients are accrued. With this trick of the low finances machine learners, you principally carry out an analogous operation to backpropagation by time. Lastly, siamese networks with shared weights additionally roughly exploit this idea.

Let’s now see the within of an LSTM [5] cell.

LSTM: Lengthy-short time period reminiscence cells

Why LSTM?

Some of the elementary works within the subject was by Greff et al. 2016 [4]. Briefly, they confirmed that the proposed variations of RNN don’t present any vital enchancment in a big scale research in comparison with LSTM. Due to this fact, LSTM is the dominant structure in RNNs. That’s why we are going to deal with this RNN variation.

How LSTM works?

We are able to write endlessly about what an LSTM cell is, or how it’s utilized in many purposes. Nevertheless, the language of arithmetic makes this world lovely and compact for us. Let’s see the maths. Don’t be scared! We are going to slowly make clear each time period, by inspecting each equation individually.

Earlier than we start, notice that in all of the equations, the load matrices (W) are listed, with the first index being the vector that they course of, whereas the second index refers back to the illustration (i.e. enter gate, neglect gate).

To keep away from confusion and maximize understanding, we are going to use the widespread notation: matrices are depicted with capital daring letters whereas vectors with non-capital daring letters. For the element-wise multiplication, I used the dot with the outer circle image, known as the Hadamard product [9] within the bibliography.

Equations of the LSTM cell

For $textbf{x}_t in R^{N}$

The LSTM cell equations had been written based mostly on Pytorch documentation as a result of you’ll most likely use the present layer in your mission. Within the unique paper, $textbf{c}_{t-1}$

Equation 1: the enter gate

The depicted weight matrices characterize the reminiscence of the cell. You see the enter $textbf{x}_t$

a) take a number of linear combos of x,h,c, and

b) match the dimensionality of enter x to the one among h and c.

The dimensionalities of h and c are principally the hidden states parameter in a deep studying framework equivalent to PyTorch (LSTM Pytorch layer documentation). For the old-school readers, hidden states had been referenced in older literature as neurons, however now this time period is deprecated.

Shifting on, the bias time period is a part of the linear layer and is just a trainable vector that’s added. The output can also be within the dimensionality of the hidden and context/cell vector [1]. Lastly, after the three linear layers from totally different inputs, we’ve got a non-linear activation perform to introduce non-linearities, which allows the training of extra advanced representations. On this case, the sigmoid perform is often used.

Equation 2: the neglect gate

Merely, equation 2 is strictly the identical factor as equation 1. Nevertheless, notice that the load matrices are totally different this time. Which means that we get a distinct set of linear combos, that characterize various things! The equations is perhaps the identical, nevertheless, we need to mannequin various things, as you will note.

Equation 3: the brand new cell/context vector

Discover that I take advantage of cell or context vector interchangeably.

We’ve got already realized a illustration that corresponds to “neglect”, in addition to for modeling the “enter vector”, f and i, respectively. Let’s preserve them apart and first examine the $tanh$ parenthesis.

Right here, we’ve got one other linear mixture of the enter and hidden vector, which is once more completely totally different! This time period is the brand new cell data, handed by the tanh perform in order to introduce non-linearity and stabilize coaching.

However we don’t need to merely replace the cell with the brand new states. Intuitively, we need to take note of earlier states; that’s why we designed RNNs anyway! That is the place the calculated enter gate vector i comes into play. We filter the brand new cell data by making use of an element-wise multiplication with the enter gate vector i (just like a filter in sign processing).

The neglect gate vector comes into play now. As a substitute of simply including the filtered enter data, we first carry out an element-wise vector multiplication with the earlier context vector. To this finish, we wish the mannequin to imitate the forgetting notion of people as a multiplication filter.

By including the beforehand described time period within the $tanh$ parenthesis, we get the brand new cell state, as proven in Equation 3.

However what concerning the output of the LSTM [5] cell in a single timestep?

Equation 4, the virtually new output

It’s easy! Let’s simply take one other linear mixture! This time, of our 3 vectors $x_t, h_(t-1), c_t$

Equation 5, the brand new context

Observe that the title in equation 4 was the virtually new output. Thus, one can calculate the brand new output (actually the brand new hidden state) based mostly on equation 5. Think about that we need to someway combine the new context vector $c_t$

Lastly, of all the photographs that go round on-line, I discovered this fascinating one to share at this level, for our visible sort co-learners:

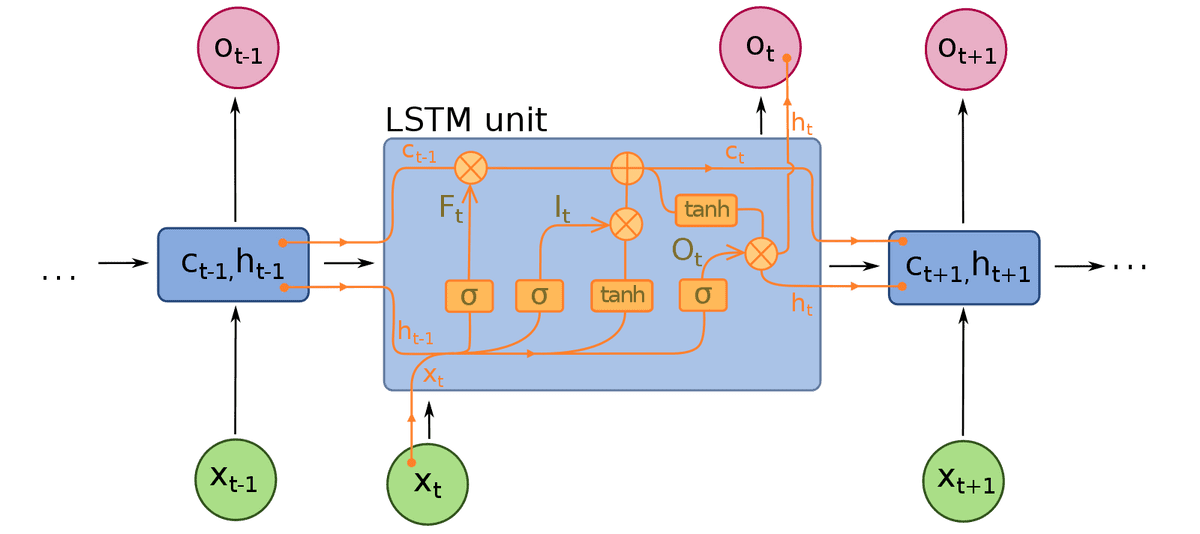
Picture is borrowed from Wiki

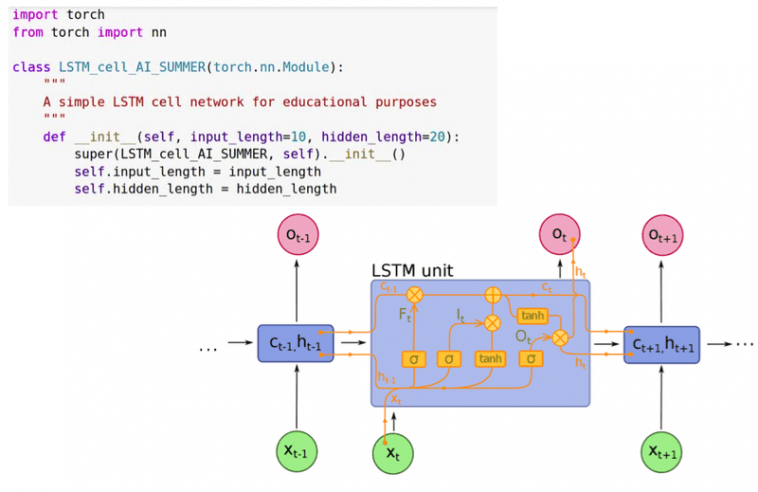
• Principally, a single cell receives as enter the cell and hidden state from the earlier timestep, in addition to the enter vector from the present timestep.

• Every LSTM cell outputs the brand new cell state and a hidden state, which will probably be used for processing the following timestep. The output of the cell, if wanted for instance within the subsequent layer, is its hidden state.

Writing a customized LSTM cell in Pytorch – Simplification of LSTM

Primarily based on our present understanding, let’s see in motion what the implementation of an LSTM [5] cell appears like. For this implementation PyTorch [6] was used.

All through the years, a less complicated model of the unique LSTM stood the take a look at of time. To this finish, trendy deep studying frameworks use a barely easier model of the LSTM. Truly, they disregard ${c}_{t-1}$

Nonetheless, it could be fascinating so that you can tweak the code based mostly on the unique implementation and evaluate the outcomes on this easy activity. The code for the simplified LSTM that Pytorch and Tensorflow are operating beneath the hood is the next:

import torch
from torch import nn
class LSTM_cell_AI_SUMMER(torch.nn.Module):
    """
    A easy LSTM cell community for instructional AI-summer functions
    """
    def __init__(self, input_length=10, hidden_length=20):
        tremendous(LSTM_cell_AI_SUMMER, self).__init__()
        self.input_length = input_length
        self.hidden_length = hidden_length
        self.linear_forget_w1 = nn.Linear(self.input_length, self.hidden_length, bias=True)
        self.linear_forget_r1 = nn.Linear(self.hidden_length, self.hidden_length, bias=False)
        self.sigmoid_forget = nn.Sigmoid()
        self.linear_gate_w2 = nn.Linear(self.input_length, self.hidden_length, bias=True)
        self.linear_gate_r2 = nn.Linear(self.hidden_length, self.hidden_length, bias=False)
        self.sigmoid_gate = nn.Sigmoid()
        self.linear_gate_w3 = nn.Linear(self.input_length, self.hidden_length, bias=True)
        self.linear_gate_r3 = nn.Linear(self.hidden_length, self.hidden_length, bias=False)
        self.activation_gate = nn.Tanh()
        self.linear_gate_w4 = nn.Linear(self.input_length, self.hidden_length, bias=True)
        self.linear_gate_r4 = nn.Linear(self.hidden_length, self.hidden_length, bias=False)
        self.sigmoid_hidden_out = nn.Sigmoid()
        self.activation_final = nn.Tanh()
    def neglect(self, x, h):
        x = self.linear_forget_w1(x)
        h = self.linear_forget_r1(h)
        return self.sigmoid_forget(x + h)
    def input_gate(self, x, h):
        x_temp = self.linear_gate_w2(x)
        h_temp = self.linear_gate_r2(h)
        i = self.sigmoid_gate(x_temp + h_temp)
        return i
    def cell_memory_gate(self, i, f, x, h, c_prev):
        x = self.linear_gate_w3(x)
        h = self.linear_gate_r3(h)
        ok = self.activation_gate(x + h)
        g = ok * i
        c = f * c_prev
        c_next = g + c
        return c_next
    def out_gate(self, x, h):
        x = self.linear_gate_w4(x)
        h = self.linear_gate_r4(h)
        return self.sigmoid_hidden_out(x + h)
    def ahead(self, x, tuple_in ):
        (h, c_prev) = tuple_in
        i = self.input_gate(x, h)
        f = self.neglect(x, h)
        c_next = self.cell_memory_gate(i, f, x, h,c_prev)
        o = self.out_gate(x, h)
        h_next = o * self.activation_final(c_next)
        return h_next, c_next

Connecting LSTM cells throughout time and house

Let’s see how LSTM’s [5] are linked in time and house. Let’s begin from the time perspective, by contemplating a single sequence of N timesteps and one cell, as it’s simpler to grasp.

As within the first picture, we join the context vector and the hidden states vector, the so-called unrolling. Equally, we join the enter sequence within the corresponding timestep, x_3 to unrolled cell 3, and many others. The dimensions of the unrolled shared-weight cells corresponds to the enter sequence timesteps. Once you assume by way of time, preserve unfolding at the back of your thoughts.

Allow us to now think about how we are able to join the cells in house. Suppose we’ve got 2 cells and a single timestep.

The two cells are kind of like a distinct layer. To know this, let’s simply assume that the context vector is encapsulated contained in the cell, whereas the hidden state vector is the output. Due to this fact, we simply have to plug the output hidden state of the primary cell because the enter vector to the following one like this:

Nevertheless, don’t confuse it with the hidden vector of the second cell as it’s fully totally different! Much less actually, the hidden output of the state of the earlier cell is linked because the enter vector to the following. The ultimate output is the final hidden cell! As a facet notice, please needless to say totally different duties might require all of the hidden layer outputs.

Validation: Studying a sine wave with an LSTM

For this proof of idea, we used the official PyTorch instance for testing LSTM cells. The code is licensed to authors’ rights. We created an interactive Google Collab pocket book so as to reproduce our outcomes. Principally, what we did is change torch.nn.LSTMcell() with our personal implementation, as offered on this tutorial. You may mess around utilizing our Google colab pocket book, however notice that the unique credit of this instance belong to the official PyTorch repo. We barely modified it to maximise understanding for strictly instructional functions. The duty is to foretell the values of sine wave sequences. The community will subsequently give some predicted outcomes, proven as sprint strains.

Merely we change:

self.lstm1 = nn.LSTMCell(1, 51)
self.lstm2 = nn.LSTMCell(51, 51)

with our personal customized implementation and mix every little thing collectively in a pocket book:

self.lstm1 = LSTM_cell_AI_SUMMER(1,51)
self.lstm2 = LSTM_cell_AI_SUMMER(51,51)

On this method, we deal with guaranteeing that the remainder of the code works okay and if we encounter an issue will probably be from our customized code. Let’s see the outcomes!

Outcomes:

Voila!

We’ve got the primary validation that proves what the implementation is right! Despite the fact that it’s not an excellent activity, you will need to carry out most of these sanity checks whenever you implement customized layers. As well as, in my humble opinion, it enhances our understanding as a result of we deal with mastering the straightforward ideas, as an alternative of simply diving in advanced duties equivalent to exercise recognition.

Bidirectional LSTM and it’s Pytorch documentation

Within the strategy that we described thus far, we course of the timesteps ranging from t=0 to t=N. Nevertheless, one pure technique to increase on this concept is to course of the enter sequence from the top in direction of the beginning. In different phrases, we begin from the top (t=N) and go backwards (till t=0). The other way processing sequence is processed by a distinct LSTM, however with the identical structure.

Earlier than you set bidirectional=True in your subsequent mission take into consideration the implications. Do you need to study temporal correlations from the top to the beginning? Does it present any which means in your downside? Are you able to make any assumption about your knowledge that might show you how to determine that? Observe that, by specifying the LSTM to be bidirectional you double the variety of parameters. Lastly, the hidden/output vector dimension can also be doubled, because the two outputs of the LSTM with totally different instructions are concatenated. A gorgeous illustration is depicted beneath:

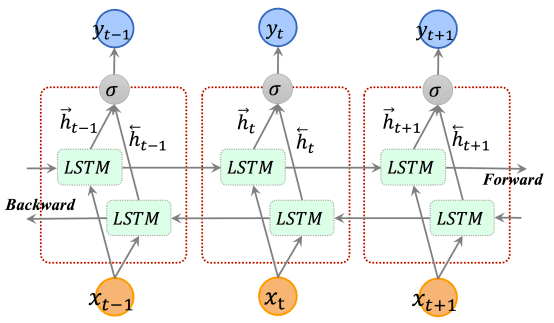
Illustration of bidirectional LSTM, borrowed from Cui et al. 2018

Lastly, let’s revisit the documentation arguments of Pytorch [6] for an LSTM mannequin. Layers are the variety of cells that we need to put collectively, as we described. Generally, dropout is added between LSTM cells.

• input_size – The variety of anticipated options within the enter x

• hidden_size – The variety of options within the hidden state h

• num_layers – Variety of recurrent layers. E.g., setting num_layers=2 would imply stacking two LSTMs collectively to type a stacked LSTM, with the second LSTM taking in outputs of the primary LSTM and computing the ultimate outcomes. Default: 1

• bias – If False, then the layer doesn’t use bias weights b_ih and b_hh. Default: True

• batch_first – If True, then the enter and output tensors are offered as (batch, seq, characteristic). Default: False

• dropout – If non-zero, introduces a Dropout layer on the outputs of every LSTM layer besides the final layer, with dropout chance equal to dropout. Default: 0

• bidirectional – If True, turns into a bidirectional LSTM. Default: False

Enter to output mappings with recurrent fashions

To keep away from doable confusions concerning recurrent layers, let’s begin by looking within the following picture:

1. The crimson bins characterize input-to-hidden states,

2. The inexperienced ones characterize hidden to hidden states, and

3. The blue ones characterize hidden to output states.

Supply: INSA machine studying course notes

The exact enter and output might be actually messy and irritating when implementing such a mannequin because the notion of time is commonly counterintuitive in deep studying. That’s the reason I want to state that recurrent fashions are actually versatile within the mapping from enter to output sequences. You simply have to switch the enter to hidden states and the hidden to output states, based mostly on the issue. By definition, LSTM’s can course of arbitrary enter timesteps. The output might be tuned by designing which outputs of the final hidden to hidden layer are used to compute the specified output.

The theoretical restrict of modeling a big dimension: Recurrency VS Convolution

Taking our dialogue one step additional, you possibly can mannequin any dimension by recurrence or by convolution. Why select one over the opposite? The hidden magic phrase that you simply search for, is the receptive subject. Relying on the issue, you desire a explicit dimension of the receptive subject. In principle, RNN’s can mannequin an infinite dimension of dimension, which signifies that their receptive subject is infinite. To this finish, we nonetheless want RNN’s for actually long run dependencies equivalent to spoken language and pure language processing. Nevertheless, it’s beneath dialogue if you should utilize pre-trained fashions with recurrent models, which is a considerable drawback. Then again, convolutional neural networks have a finite receptive subject [11]. Nonetheless, there are quite a lot of tips that you are able to do to extend it, equivalent to dilated convolutions.

Dialogue and conclusion

As a ultimate notice, the concept of recurrent neural networks might be generalized in a number of dimensions, as described in Graves et al 2007 [7]. In principle, as an alternative of 1D enter unrolling we might have a 2D or typically, N-dimensional unrolling. This work was offered by Alex Graves and it’s a tremendous idea in my humble opinion. One other fascinating strategy is making use of recency in graph-structured knowledge [8].

In a compact sentence, I want to say that the magic of RNNs lies within the capacity to mannequin effectively long-term dependencies through contextual data. Given the very fact you understood the primary ideas, you possibly can proceed to a phenomenal TensorFlow tutorial by Google, that presents a really detailed strategy for textual content era with RNNs.

For additional studying, I’d recommend this superior weblog publish [10] that gives recommendations on bettering the efficiency in recurrent layers. Alternatively, you possibly can watch the superior speak that was just lately launched from DeepMind:

However, if you’d like a extra holistic strategy in recurrent networks there is a superb course from Coursera, which we extremely suggest. Having mentioned that, we imagine that we offered assets for all of the several types of learners. Please refer right here [3] for a extra detailed evaluation on RNN optimization.

To conclude, this text serves as an illustration of a number of ideas of recurrent neural networks. We fastidiously constructed upon the concepts, with the intention to perceive sequence fashions that deal with time-varying knowledge. We did our greatest to bridge the gaps between RNN’s in pc imaginative and prescient. Within the subsequent half, we are going to see beneath the hood of a GRU cell and analyze them facet by facet.

Cited as:

@article{adaloglou2020rnn,
    title   = "Recurrent neural networks: constructing a customized LSTM cell",
    writer  = "Adaloglou, Nikolas and Karagiannakos, Sergios ",
    journal = "https://theaisummer.com/",
    12 months    = "2020",
    url     = "https://theaisummer.com/understanding-lstm"
  }

References

[1][understanding lstm networks](https://colah.github.io/posts/2015-08-Understanding-LSTMs/), Cohan’s weblog, 2015

[2][a recipe for training neural networks](http://karpathy.github.io/2019/04/25/recipe/), Andrej Karpathy weblog, 2019

[3][pptimizing rnn performance](https://svail.github.io/rnn_perf/), Half I: Investigating efficiency of GPU BLAS Libraries, Erich Elsen, Baidu Silicon Valley AI Lab

[4] Greff, Ok., Srivastava, R. Ok., Koutník, J., Steunebrink, B. R., & Schmidhuber, J. (2016). LSTM: A search house odyssey. IEEE transactions on neural networks and studying techniques, 28(10), 2222-2232.

[5] Hochreiter, S., & Schmidhuber, J. (1997). Lengthy short-term reminiscence. Neural computation, 9(8), 1735-1780.

[6] Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., … & Desmaison, A. (2019). PyTorch: An crucial model, high-performance deep studying library. In Advances in Neural Info Processing Methods (pp. 8024-8035).

[7] Graves, A., Fernández, S., & Schmidhuber, J. (2007, September). Multi-dimensional recurrent neural networks. In Worldwide convention on synthetic neural networks (pp. 549-558). Springer, Berlin, Heidelberg.

[8] Agrawal, R., de Alfaro, L., & Polychronopoulos, V. (2017, March). Studying from graph neighborhoods utilizing lstms. In Workshops on the Thirty-First AAAI Convention on Synthetic Intelligence.

[9] Horn, R. A. (1990, Could). The Hadamard product. In Proc. Symp. Appl. Math (Vol. 40, pp. 87-169).

[10] Danijar Hafner, Suggestions for Coaching Recurrent Neural Networks, 2017

[11] Araujo, A., Norris, W., & Sim, J. (2019). Computing Receptive Fields of Convolutional Neural Networks. Distill, 4(11), e21.

[12] Cui, Z., Ke, R., Pu, Z., & Wang, Y. (2018). Deep bidirectional and unidirectional LSTM recurrent neural community for network-wide visitors velocity prediction. arXiv preprint arXiv:1801.02143.

* Disclosure: Please notice that among the hyperlinks above is perhaps affiliate hyperlinks, and at no further value to you, we are going to earn a fee if you happen to determine to make a purchase order after clicking by.